Reference no: EM132655556

MATL972 Selection and Design of Material - University of Wollongong

QUESTION 1:

You are asked to select a suitable material for producing a skateboard deck. Skateboard decks need to be strong, stiff, lightweight and, preferably, cheap. Most decks are simple solid rectangular cross-section beams, loaded in 3-point bending (as shown in the figure below). The deck length and width are fixed, while the deck thickness, t, is a free variable. Answer the following questions:

(a) Derive the performance metric and materials index equations for the following:

(i) The mass of the skateboard deck (between the front and back wheels) for a given stiffness.
(ii) The mass of the skateboard deck (between the front and back wheels) for ensuring sufficient strength.

The following equations may be needed for the derivations:
Stiffness: S = F/δ = 48EI/L³

Strength (force to cause failure):

F_f = 4Zσ*/L

(b) Use the appropriate materials property chart in the Appendix to select the four materials that would give the lightest decks that meet the desired stiffness constraint. Explain the steps taken in your selection process.

(c) Use the appropriate materials property chart in the Appendix to select the four materials that would give the lightest decks that meet the desired strength constraint. Explain the steps taken in your selection process.

(d) Skateboard decks need to be both stiff and strong. Use a graphical method to identify the three lightest deck materials that satisfy both the strength and stiffness constraints. Explain the selection procedure used.
Use the following values in your assessment:

L = 0.8 m; w = 0.2 m; F = 1500 N; δ = 0.05 m

(e) Secondary objectives for the skateboard are to minimise cost and minimise the deck thickness. Comment on the suitability of the three materials identified in Question 1(d) in relation to these additional objectives. Which one of the three materials identified in Question 1(d) would you choose for the skateboard deck? Explain why.

QUESTION 2:

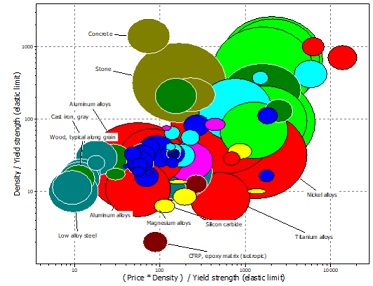
The figure below explores the trade-off between minimising mass and price for a component loaded in tension. The lightest material is the one with the lowest value of ρ /σ_y, and the material with the lowest price is the one with the lowest value of C_mρ /σ_y.
where: Cm is the material cost per kilogram, ρ is the material density, and σ_y is the yield strength.

(a) Sketch the trade-off surface on the figure above and explain what it means.

(b) Write an expression for the penalty function Z and explain what it means including a definition of the exchange constant.

Attachment:- Selection and Design of Material.rar