User Account

All Pages

Identify any vertical and horizontal asymptotes

Assignment Help Algebra
Reference no: EM131344301

QUESTION 1
Find the domain of the function f(x) = 8/ (x-6)

Domain: all real numbers x except x=6

Domain: all real numbers x except x=8

Domain: all real numbers x except x = -8

Domain: all real numbers x

Domain: all real numbers x except x = -6

QUESTION 2
Find the domain of the function f(x) = 8x2 / (x2 -49)

Domain: all real numbers x except x = 7

Domain: all real numbers x except x = ±49

Domain: all real numbers x except x = ±8

Domain: all real numbers x except x = -7

Domain: all real numbers x except x = ±7

QUESTION 3
Determine the domains of f and g.

f(x) = (x2 -36) / (x + 6), g(x) = x - 6

Domain of f: all real numbers x except x = -6
Domain of g: all real numbers x

Domain of f: all real numbers x except x = ±6
Domain of g: all real numbers x

Domain of f: all real numbers x except x = ±36
Domain of g: all real numbers x except x=6

Domain of f: all real numbers x except x = 6
Domain of g: all real numbers x

Domain of f: all real numbers x except x = ±6
Domain of g: all real numbers x except x=6

QUESTION 4
Find the domain of f(x) = (x - 9) / (x2 - 81)

all real numbers except x = -9

all real numbers except x = 81

all real numbers except x = 9

all real numbers except x = 9 and x = -9

all real numbers

QUESTION 5
Find the domain of the function and identify any vertical and horizontal asymptotes.

f(x) = (2 +x) / (2 -x)

Domain: all real numbers x except x = 2
Vertical asymptote: x = 2
Horizontal asymptote: y = -1

Domain: all real numbers x
Vertical asymptote: x = -2
Horizontal asymptote: y = 0

Domain: all real numbers x except x = 0
Vertical asymptote: x = 0
Horizontal asymptote: y = -1

Domain: all real numbers x except x = 2
Vertical asymptote: x = 0
Horizontal asympotote: y = -2

Domain: all real numbers x except x = -2
Vertical asympotote: x = 0
Horizontal asympotote: y = 2

QUESTION 6
Find the domain of the function and identify any vertical and horizontal asympototes.

f(x) = 2x2 / (x + 6)

Domain: all real numbers x except x = 0
Vertical asympotote: x = 0
Horizontal asympotote: y = -2

Domain: all real numbers x except x = -6
Vertical asympotote: x = -6
Horizontal asympotote: No horizontal asymptote

Domain: all real numbers x except x = 6
Vertical asympotote: x = 6
Horizontal asympotote: No horizontal asympotote

Domain: all real numbers x except x = 6
Vertical asympotote: x = 6
Horizontal asymptote: y = 2

Domain: all real numbers x
Vertical asymptote: x = -6
Horizontal asymptote: y = 0

QUESTION 7
Find the domain of the function and identify any vertical and horizontal asympototes.

f(x) = (9x2 + 8) / (9x2 + x + 9)

Domain: all real numbers x
Vertical asympotote: No vertical asymptote
Horizontal asymptote: y = 9

Domain: all real numbers x except x = 0
Vertical asymptote: x = 0
Horizontal asymptote: y = -8

Domain: all real numbers x
Vertical asymptote: x = -9
Horizontal asymptote: y = 0

Domain: all real numbers x except x = 9
Vertical asymptote: No vertical asymptote
Horizontal asymptote: No horizontal asymptote

Domain: all real numbers x except x = 9
Vertical asymptote: x = 9
Horizontal asymptote: y = 8

QUESTION 8
Determine the value that the function f approaches as the magnitude of x increases.

f(x) = (2x - 1) / (x - 3)

∞

-3

2

-1

0

QUESTION 9
Simplify f and find any vertical asymptotes of f.

f(x) = (x2 - 36) / (x + 6)

x+6; Vertical asymptote: none

x-6; Vertical asymptote: x=6

x-6; Vertical asymptote: none

x-36; Vertical asymptote: x=6

x-36; Vertical asymptote: none

QUESTION 10
Simplify f and find any vertical asymptotes of f.

f(x) = [x2 (x + 3)] / (x2 + 3x)

x+3; Vertical asymptote: x = -3

x; Vertical asymptote: none

x; Vertical asymptote; x = -3

x - 3; Vertical asympotote: none

x2; Vertical asympotote: none

QUESTION 11
Determine the value that the function f approaches as the magnitude of x increases.

f(x) = 4 - (3/x)

3

-3

4

-4

-3.67

QUESTION 12
Find the domain of the function and identify any vertical and horizontal asymptotes.

f(x) = (x + 2) / (x2 - 4)

The domain is all real numbers x except x = ±2. There is a vertical asymptote at x = -2, and a horizontal asymptote at y = 0.

The domain is all real numbers x except x = ±2. There is a vertical asymptote at x = -4, and a horizontal asymptote at y = 0.

The domain is all real numbers x except x = ±4. There is a vertical asymptote at x = -4, and a horizontal asymptote at y = 0.

The domain is all real numbers x except x = ±2. There is a vertical asymptote at x = 2, and a horizontal asymptote at y = 0.

The domain is all real numbers x except x = ±4. There is a vertical asymptote at x = -2, and a horizontal asymptote at y = 0.

QUESTION 13
Determine the equations of any horizontal and vertical asymptotes of

f(x) = (x2 - 1) / (x2 + 4x -5)

horizontal: y = 5; vertical: x = 0

horizontal: y = 1; vertical: x = -5

horizontal: y=1; vertical: x=1 and x = -5

horizontal: y = -1; vertical: x = -5

horizontal: y = 0; vertical: none

QUESTION 14
Determine the equations of the vertical and horizontal asymptotes of the graph of the function.

f(x) = 2x2 / (x2 - 9)

horizontal: x = -2; vertical: y = 3 and y = -3

horizontal: y = 2; vertical: x = 3 and x = -3

horizontal: y = -3; vertical: x = 2

horizontal: y = 2; vertical: x = 3

horizontal: x = 3 and x = -3; vertical: y = -2

QUESTION 15
Simplify f and find any vertical asymptotes of f.

f(x) = (6x - 1) / (6x2 - x)

x2; Vertical asymptote: x = 0

x-1: Vertical asymptote: none

x: Vertical asymptote: x=0

x:Vertical asymptote: none

1/x: Vertical asymptote: x=0

QUESTION 16
Identify all intercepts of the function.

f(x) = 1 / (x - 4)

y-intercept: (0,-1/4)

y-intercept: (0,1/4)

y-intercept: (0,4)

y-intercept: (4,0)

y-intercept: (0,-4)

QUESTION 17
Identify all intercepts of the following function:

g(x) = (x2 +3) / x

x-intercepts: (±3,0)

no intercepts

x-intercepts: (-3,0)

x-intercepts: (0,0)

x-intercepts: (3,0)

QUESTION 18

Select the correct graph of the function

f(x) = 6 / (x + 3)

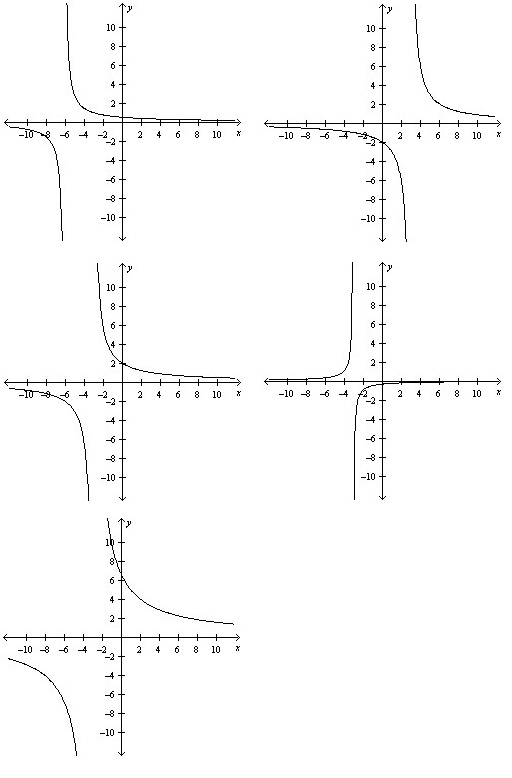
598_Graph1.jpg

QUESTION 19

Select the graph of the rational function. (Plotted additional solution points as needed.)

g(x) = 1 / (2 -x)

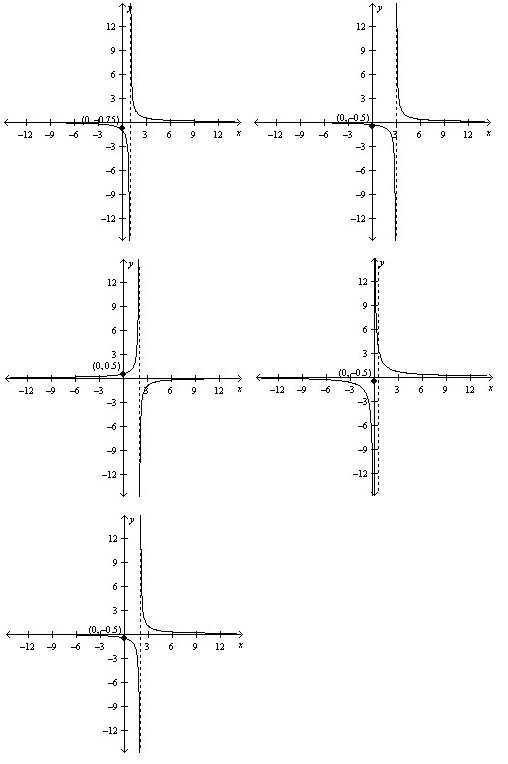
1190_Graph2.jpg

QUESTION 20

The cost C (in millions of dollars) of removing p% of the industrial and municipal pollutants discharged into a river is given by

C = 245p / (100 -p), 0 ≤ p < 100

According to this model, would it be possible to remove 100% of the pollutants?

No. The function is undefined at P = 100.

Yes

Reference no: EM131344301

Questions Cloud

Hydrogen and oxygen gas mixture : The "pop" bottle demonstration requires that hydrogen and oxygen gas mixture be ignited by a flame. True or False: This means that the reaction of hydrogen gas and oxygen gas to form water is endothermic. Support the answer.
Mixture of hydrogen and oxygen gases or water : Which is lower in energy in this reaction: a mixture of hydrogen and oxygen gases or water? how do you know that this is true? Explain and sketch an energy level diagram for this reaction to help support the answer.
Heat of combustion of sucrose : 1.150g of sucrose goes through combustion in a bomb calorimeter. If the temperature rose from 23.42 to 27.64 degrees Celsius and the calorimeter constant was 4.9kJ/ Celsius, determine the heat of combustion of sucrose in kJ/mol.
Difference between ionic bonding and covalent bonding : What is the difference between ionic bonding and covalent bonding? Give an example of each type. Which type of bonding is more polar in nature and why?
Identify any vertical and horizontal asymptotes : Find the domain of the function and identify any vertical and horizontal asymptotes. Determine the value that the function f approaches as the magnitude of x increases. Simplify f and find any vertical asymptotes of f.
Calculate the percent of kci in the unknown mixture : a. Assuming that the original unknown mixture contained KCIO3 and KCI with combined mass of 2.1307g, calculate the mass of KCI in the unknown mixture. b. Calculate the percent of KCIO3 in the unknown mixture. c. Calculate the percent of KCI in the ..
Discuss the positives and negatives surrounding opioid use : Write a well-developed essay in which you discuss the positives and negatives surrounding opioid use. Provide examples and include the following:The advantages and disadvantages of the use of semisynthetic opioid analgesics (oxymorphone, hydrocodo..
Molecules in the stratosphere absorb : Ozone molecules in the stratosphere absorb much of the harmful UV radiation from the sun.  Typically, the temperature and pressure of ozone in the stratosphere are -23 °C and 1.0 torr, respectively. How many moles of ozone are present in 100. L of..
Calculate the new volume using the ideal gas law : (a) The volume of this balloon will (increase/decrease) (slightly/dramatically). In thisexperiment (pressure/temperature/amount of gas) (is/are) constant. (b) Calculate the new volume using the ideal gas law.

Reviews

Write a Review

Algebra Questions & Answers

  Solve the linear model

Select five values for x to plug into the linear function, P(x)=10x-7 and prepare a table of values

  Identify the sample and suggest a population

Identify the sample and suggest a population

  Evaluate the ratios

Evaluate the ratios and check are the ratios equivalent.

  Define variables and profit function

Define variables and profit function

  Make a linear equation

Assume you have a lemonade stand, & when you charge $1 per cup of lemonade you sell 50 cups. But when you raise your price to $2 you only sell 25 cups. Make an equation for the number of cups you sell as a function of the price you charge. Denote "C"..

  Classify linear and non linear functions

For each of the relationships given below, describe whether you think it is best explained by a linear function or a non-linear function.

  Which of the following are functions

Which of the following are functions?  The two problems, i.e., 1 & 3, are multi part relations consider all parts when determining whether or not these relations are functions. Explain your reason for 1, 2, & 3.

  Using venn diagram for solving word problems

Using venn diagram for solving word problems.

  Joint probability density function

The joint probability density function.

  Applications of combination

Applications of combination

  Solving problems using venn diagram

Solving problems using venn diagram.

  Solving problems into equation

Solving problems into equation.

Free Assignment Quote

Assured A++ Grade

Get guaranteed satisfaction & time on delivery in every assignment order you paid with us! We ensure premium quality solution document along with free turntin report!

Submit Assignment

Academics

Major Subjects

Majors

Get In Touch

whatsapp: +1-415-670-9521

Phone: +1-415-670-9521

Email: [email protected]

TERMS & POLICIES

HELP & SUPPORT

All rights reserved! Copyrights ©2019-2020 ExpertsMind IT Educational Pvt Ltd