Reference no: EM132649014

EXERCISE 1. Consider the coin toss space (Ω_∞, f_∞, P_∞) and let Z10 (ω) de-note the position of the random walk after 10 periods, associated with the outcome ω ∈ Ω_∞ Prove that Z₁₀ is a well-defined r. v. on  Ω_∞ and give its distribution law. Calculate P_∞({Z₁₀ ≥ 0 }) and P_∞({2 ≤ Z₁₀ < 5}).

Now we turn to some common methods for specifying distribution laws of real-valued random variables. Any such law is a probability measure on B(R), and, ^o-•(1.59) as we already know, there is a one-to-one correspondence between probability measures on B(R) and increasing cadlag functions F: R|-> R such that F(-∞) = 0 and F(+∞) = 1.

EXERCISE 2. DISTRIBUTION FUNCTIONS: Let X be any random variable and let L_x de¬note its distribution law. The distribution function of X (alias: the cumulative distribution function of X) is given by

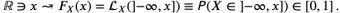
Thus, the law of X can be expressed L_X = dF_x, and if the random variable X is understood from the context, we may write L and F instead of L_x and F_x.

EXERCISE 3. Give the distribution function of the random variable Z₁₀ from exercise 1.

EXERCISE 4. Prove that the distribution function, F_x, associated with any random variable X, is cadlag, increasing, and such that lim_x→-∞ F_x(x) = 0 and im_x→+∞ F_x(x) = 1. In addition, prove that F_x is continuous that is, it is left-continuous) if and only if the distribution law Lx is nonatomic. Is it possible for the distribution law L_x and the Lebesgue measure A to be singular to one another (L_x  ⊥ A) if the distribution function F_x is continuous?

EXERCISE 5. Let X  ∈ N (a, σ²) and let θ ∈ R. Prove that

E[e^-θ X-a/σ² -1/2 |θ|²/σ²]= E[e^θ X-a/σ² -1/2 |θ|²/σ²] = 1

for every choice of the parameters a, θ ∈ R and  σ ∈ R₊₊.

EXERCISE 6: Consider two sequences of random variables, X = (X_i)i ∈ N and Y = (Y_i)_i∈N, not necessarily defined on the same probability space, and suppose that these two sequences are statistically indistinguishable, in the sense that from observing either sequence it would not be possible to tell whether the observed sequence is X or Y.⁶⁹ Prove that if either of these two sequences converges in probability (converges a.s.), then the other one must also converge in probability (must converge a.s.).

EXERCISE 7: Let A be any family of random variables and suppose that there is an integrable r.v., η, that dominates the family A, in that I |ξl ≤ |η|P-a.s. for all ξ ∈ A. Prove that the family at is uniformly integrable.

This statement admits the following generalization: if A and B are any two families of random variables, defined on the same probability space, if the family a is uniformly integrable, and if B dominates A, in the sense that for every ξ ∈ A there is some η ∈ B such that lξ| ≤ |η| (a.s.), then the family A must be uniformly integrable as well.

Note: Need only EXERCISE 3, 4, 5, 6, 7 Only.