Reference no: EM132559718 , Length: word count:1500

Part 1:

Problem 1:

You've come across research explaining the recent credit bubble by obesity. The research provided a strong correlation as proof that the credit bubble was in fact caused by people gaining weight, as seen in the following chart.

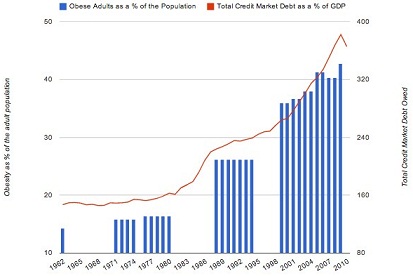
Critically evaluate the research findings and point out any potential problems with the methodology.

Problem 2

You are an investment analyst and you are trying to build a model explaining a recent uptick in inflation. You have identified three variables which influence inflation - unemployment, median salary change, and the change in the price level of imports. The regression equation you have constructed is as follows:

y = β₁x₁ + β₂x₂ + β₃x₃

Where:

y - Inflation

x1 - Unemployment

x2 - Median salary change

x3 - Change in the price level of imports

While testing for the significance of your regression model, you have determined that all slopes β are significantly different from zero, but x1 and x2 (unemployment and median salary change) are not independent, and there is a statistically significant relationship between these two variables.

Critically evaluate this problem and propose a solution.

Part 2:

Problem 1:

Many macroeconomic indicators, such as unemployment, are routinely seasonally adjusted before being published by statistical offices. Here is an example of such a time-series cleaning for unemployment in the United Kingdom according to Eurostat's methodology:

"Unemployment data is collected in a household survey and a 3-month moving average is applied to remove any non-repeating volatility. The seasonal component is then removed from the time-series on an annual basis."

Find how unemployment is calculated in your country and critically asses the limitation of the model. Evaluate how the method used makes unemployment more or less representative of the real situation on the job market.

Problem 2:

Equity and government bonds are a natural pair in any well diversified portfolio, because the price of stocks tends to increase in value, while bonds tend to decrease when times are good. The opposite is true during downturns.

Critically evaluate how this relationship works, and use mean-variance analysis to explain how it can be used to lower overall risk in a portfolio. Use examples.

Part 3:

Problem 1:

James is a farmer who owns 8 acres of agriculture land. He can plant the land with maize and sugarcane. He can earn $5,000 for every acre he plants with maize and $3,000 for every acre he plants with sugarcane. His use of a necessary pesticide is limited by government regulations to 10 gallons for his entire 8 acres.

Maize requires 2 gallons of pesticide for every acre planted and sugarcane requires just 1 gallon per acre.

Given the situation James is facing, he wants to divide the land in a combination of maize and sugarcane plantations, such that he could maximise the profit he receives from his farming business while complying with the government regulations on pesticide use.

One way James could achieve his goal is to try the "trial and error" method, by trying different combinations of maize and sugarcane and seeing how much profit he can make from each combination.

However, James' daughter, Sara, studies linear programming and she helped her father to solve the problem using linear programming.

Question: what combination of maize and sugarcane plantation did Sara suggest to James, and what was the final profit that James achieved with that combination?

Problem 2:

You are the finance manager of the firm Sunderland Plastics Limited, which produces two products (X1 and X2) using two different machines (M1 and M2). Each unit of X1 requires 4 hours of processing time on M1 and 2 hours of processing time on M2. Each unit of X2 that gets produced requires a 1 hour processing time on M1 and 1.5-hour processing time on M2.

The firm has an available processing time of 40 hours of M1 and 30 hours of M2 available this week. The firm also meets the non-negativity constraints. Your task is the following:
The firms makes a net profit of 400 USD from 1 unit of product X1 and 100 USD from 1 unit of product X2

1) Formulate a linear programming problem in the standard form for Sunderland Plastics Limited.
2) Solve the problem graphically and show what combination of the products X1 and X2 the firm should produce to maximise its profit while satisfying the constraints it is facing. How much profit will the firm make?