ELE3105 Computer Controlled Systems Assignment

Assignment Help Electrical Engineering

Reference no: EM132471953 , Length: 5 pages

ELE3105 - Computer Controlled Systems - University of Southern Queensland

Ships at sea undergo motion about their roll axis. Fins called stabilizers are used to reduce this roll motion. The stabilizers can be positioned by a closed-loop roll stabilizing system shown below

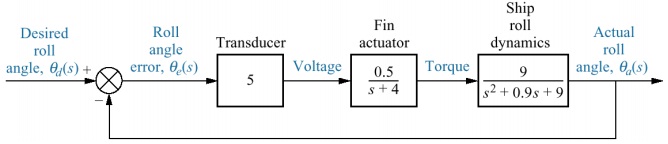
682_Closed-loop roll stabilizing system.jpg

where the transducer works like a proportional (P) controller. If given the open-loop transfer function

G(s)H(s) = (22.5/((s+4)(s²+0.9s+9))x1

Question 1. Analytically find the open-loop response c(t) to a unit impulse input, show your mathematical working and plot this open-loop system response.

Question 2. Based on sampling theorem, determine a suitable sample interval T for the following parts of the assignment and show your reasoning. (Hint: Use Bode plots of G(s)H(s) to determine the system's cut-off frequency. At cut-off frequency the magnitude plot is about 3dB below the magnitude of the low frequency. The cut-off frequency can be considered as the highest frequency component).

Question 3. If the G(s) can be simplified into G₁(s) 22.5/4(s²+0.9s+9), derive the discrete-time system transfer function GHP(Z) from G1(s) and show your mathematical working.

Question 4. Design a digital Proportional (P) controller to form a unit feedback control system, and optimise its parameter P with respect to the performance criterion IAE using the steepest descent minimisation process. Simulate the P controller system and plot its response for a unit step input (The performance criterion IAE = ∑_k=0^M| e_k|).

(Please provide the plots that show the initial and the final/optimal responses).

Question 5. If the P controller is replaced with a PID controller, using the steepest descent minimisation process again to optimise the PID controller with respect to the performance criterion IAE = ∑_k=0^M| e_k | for a unit step input. (Please also provide the plots that show both the initial and the final/optimal responses).

Reference no: EM132471953

Questions Cloud

Explain rules of english to be applied when writing business : Explain the rules of English to be applied when writing business documents (e.g.: correct grammar and spelling) and please explain two (2) additional rules

Determine designing and planning a new business document : Determine designing and planning a new business document. Be sure to consider what information you would gather to clarify the purpose and inclusions

Determine the taxable amount of social security benefits : Determine the taxable amount of social security benefits for the following situations. If required, round your answers to the nearest dollar.

What type of reaction is health care provider concern about : What type of reaction is the health care provider concerned about, and why? What would you tell EO's parents to look for when they are assessing for a reaction?

ELE3105 Computer Controlled Systems Assignment : ELE3105 Computer Controlled Systems Assignment Help and Solution, University of Southern Queensland - Assessment Writing Service

What can we do as professional nurses to bridge the gap : Identify a specific reading or a video you viewed over the last few weeks related to Gender Vulnerability that identifies the current state of our nursing.

What is the balance of the equity investment at end of year : How much equity income should the investor report for the year? What is the balance of the Equity Investment at the end of the year?

Discuss the epidemiology of ibs : Discuss the epidemiology of IBS? Discuss First line and second line drug therapy for IBS. Please include pharmacotherapeutic information.

Determine the classification for the cost as a product cost : Determine the classification for the cost as a product cost, further classify it as direct material (DM), direct labor (DL), or manufacturing overhead (MOH).

User Account

All Pages