Reference no: EM132365478

Question 1 - Let (X_n, n = 0, 1, 2, . . .) be a (time-homogeneous) Markov chain with state space E = {-1, 0, 1}, (one-step) transition matrix

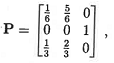
and initial distribution defined by P(X₀ = x) = (x + 2)/6 for x ∈ E.

(a) Calculate P(X₂ = 1| X₀ = 0) and P(X₂ = 1).

(b) Determine EX₂ and Var(X₂).

(c) Find all stationary distributions. Which (if any) are limiting?

(d) Write a computer program to simulate realisations of this chain. Denoting independent realisations of the state after two steps as X₂^(k) for k = 1, . . ., N, using N = 10³ estimate:

Provide your estimates, estimates of their corresponding standard errors, and your computer code.

Question 2 - Suppose we have a (time-homogeneous) Markov chain on a finite state space E. Show the following results.

(a) For x, y ∈ E, if x → y but r_yx = Py(τ_x < ∞) < 1 then x is transient.

(b) If x ∈ E is transient, then all y ∈ E for which x ↔ y are transient. That is, transience is a class property.

(c) If a communicating class C ⊂ E is not closed, then all states x ∈ C are transient.

Question 3 - Let (X_n, n = 0, 1, 2, . . .) be a (time-homogeneous) Markov chain with state space E = {0, 1, . . . , M} for some finite integer M ≥ 3, initial distribution specified by P(X₀ = 0) = 1, and (one-step) transition probabilities p_ij = P(X₁ = j|X₀ = i) given by

(a) Draw the transition probability graph of the chain.

(b) Identify the communicating classes of the chain.

(c) Classify each communicating class of states with all of the following labels that may apply to it: transient, recurrent, closed, and absorbing.

(d) For each communicating class, classify it either as aperiodic or as periodic and determine its period.

(e) For each aperiodic recurrent communicating class, treat it as a distinct Markov chain and determine its (unique!) stationary (and limiting) distribution.

(f) Let C be the number of aperiodic recurrent communicating classes, and denote by C_k ⊆ E the corresponding subset of states and π_k, k = 1, . . . , C the corresponding stationary distribution from (e) collected in to a row vector with length equal to |E| with zeros placed on all entries outside of C_k. Determine all the possible limiting distributions of the chain.

(g) Continuing, in terms of these π_k, write a general expression for all the possible stationary distributions of the chain.

(h) Let M → ∞ and repeat (c) with the label recurrent replaced by the pair of labels positive recurrent and null recurrent.

(i) Continuing, use local balance to find a stationary distribution of a countably infinite (null or positive) recurrent communicating class.

Question 4 - An extremely useful application of an irreducible positive recurrent Markov chain having unique stationary distribution that is also limiting lies in Markov chain Monte Carlo (MCMC). The idea is to construct such a Markov chain (X_n, n = 0, 1, . . .) whose unique limiting distribution can be customised. A celebrated approach is to construct the so-called Metropolis-Hastings chain. On a given state-space E, the ingredients are a proposal distribution for proposed states (Y|X_n = x) encoded via q_xy = P(Y = y|X_n = x) for all x, y ∈ E and a target distribution p_x = c · P(Z = x) for x ∈ E, where c > 0 is an arbitrary constant that need not be specified, and Z is a random variable which has the desired target distribution but is difficult to sample from by other means.

These ingredients are combined though the acceptance probabilities

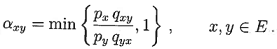
The Metropolis-Hastings chain evolves as follows:

(i) Given the current state of the chain is x, a proposal state y is drawn from the proposal distribution.

(ii) The chain moves to the proposed state y with probability a_xy; otherwise, it stays in the current state x.

This question deals with some of the theory and practice of this approach.

(a) Show that the transition density of the Metropolis-Hastings Markov chain satisfies local balance with (p_x, x ∈ E) as the stationary distribution.

(b) Determine a sufficient condition on the q_xy and p_x which will ensure that (p_x, x ∈ E) is the unique limiting distribution of the chain.

Now, let x = (x₁, . . . , x_J) be a vector with each x_i ∈ {- 1, 1} and let E = {-1, 1}^J  be the set of all such vectors. Suppose we wish to generate random vectors from a particular discrete multivariate Boltzmann pdf of the form

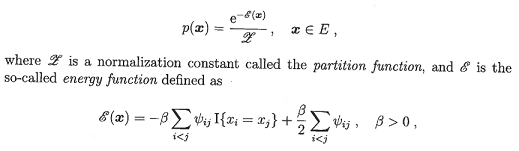
where ψ_ij are the entries of a given J x J symmetric matrix containing only zeros and ones.

Specifically, we wish to simulate realizations from the Ising model, which can be described as follows. Consider the two-dimensional lattice {1, . . . , n} x {1, . . . , n} with J = n² spatial positions (sites), and the entries of the matrix ψ_ij are 1 if sites i and j on the lattice are nearest neighbours, and 0 otherwise. Let {1, . . . , J} with J = n² be the enumeration of all the sites. To each site i we can assign a colour x_i out of two possible colours {-1, 1}. Then, the configuration of the lattice is described by the vector x = (x₁, . . . , x_j).

(c) Design a Metropolis-Hastings chain with limiting distribution p(x).

(d) On a computer, implement your sampler with some lattice dimension n ≥ 100 and use it to estimate the partition function and mean total energy for the Ising model over a range of β ∈ [0, 1]. Provide a realization your chain after a large number of steps near β = 0.11. Plot your estimates for the partition function and mean total energy as a function of β. Also provide your computer code.

Attachment:- Assignment Questions.rar