Determine the total change in length of the column

Assignment Help Other Subject

Reference no: EM132644981

Question 1. The structure below is loaded with the force as indicated. The critical components of the structure are Bar DF, BD and pin at D. The pin D is a double shear joint. The ultimate shear stress of the material is 300 MPa. Assume, safety factor on shear stress is 3. The cross-sectional area of the bars FD and BD are 2000 mm2, yield strength of the bar material is 210 MPa.
Find the following:

a. For the given information in the figure, calculate the required diameter of the pin for joint D.
b. The bars are made with a material that has yield strength of 210 MPa in tension or compression. Calculate the axial stress in bar DF and bar BD, and the safety factors for the bars.
c. Is the structure safe ?

Question 2. A column is fabricated from square structural steel tubing as shown in the figure, having a modulus of elasticity E = 210 GPa is subjected to axial loading. Determine the total change in length of the column.

Question 3. A state of plane stress consists of a tensile stress of σx=3 MPa, σy=5 MPa, and τxy=-7 MPa
a. Draw the original unrotated element and the corresponding 2-D Mohr's circle construction showing the x-face and y-face coordinates.
b. Calculate the principal stresses, σ1 and σ2 and their corresponding principal angles, θp1,θp2 and show all of these on your Mohr's circle construction and a properly oriented stress element.
c. Calculate the maximum shear stresses, ±τMAX and their corresponding angles of maximum shear stress, θs1,θs2 and show all of these on your Mohr's circle construction and a properly oriented stress element.

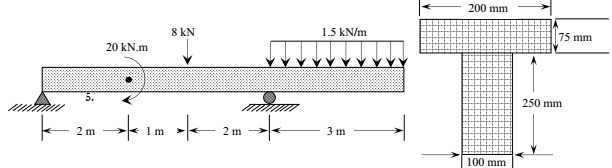
Question 4. A T-shaped cross-sectional beam is loaded as shown in the figure. Determine the following:
a. Sketch the internal shear force and bending moment diagrams for the beam.
b. Calculate the maximum magnitude of the bending stress. Indicate where this occurs on the cross-section and along the length of the beam.
c. Calculate the transverse shearing stress at the centroid of the cross-section using the maximum magnitude of the transverse shear force.

Question 5. Determine the state of stress at point A. Indicate the component of stress in the proper directions on the block provided. Is the state of stress indicated on the block a principal stress state?

Question 6. A beam is supported by ‘different support systems' as shown in the figures. Take, E and I as the beam constants. Find the deflection and slope equations of the beam for all three cases.

Note: Write down the boundary conditions, solve for reactions, solve for constants of integration, and then complete the deflection and slope equations.

Reference no: EM132644981

Questions Cloud

Discuss the deferred consideration : Discuss the difference between deferred consideration and contingent consideration. Pelhams Ltd and Selbourne Ltd as at 30 June 2019.

Compute monthly payments for the loan from furniture store : Financial Planning Exercise - Comparing payments and APRs of financing alternatives. Compute the monthly payments for the loan from the furniture store

What is the company wacc : You are given the following information for Watson Power Co. Assume the company's tax rate is 25 percent.

What is the true cost of building the new assembly : What is the true cost of building the new assembly line after taking flotation costs into account? (Do not round intermediate calculations

Determine the total change in length of the column : Calculate the axial stress in bar DF and bar BD, and the safety factors for the bars - Determine the total change in length of the column.

What is the company pretax cost of debt-viserion inc : Viserion, Inc., is trying to determine its cost of debt. The firm has a debt issue outstanding with 27 years to maturity that is quoted

Classical Economics Versus Keynesian Economics : Compare and contrast classical economics and Keynesian economics. What are the major differences between them?

Calculate the net interest expense to be reported : Calculate the net interest expense to be reported for this note and related swap transactions as at December 31, 2020 and 2021

Define right of search in brief : Write a 250-300-word paper in which you define right of search, Examine how each of this term may apply to the following: Stop-and-frisk.

User Account

All Pages