Reference no: EM133923129

Question 1. Fig. Q-1 shows half of a circular wall that is subjected to hoop tension, N_Ed of 600 kN per metre height, due to quasi-permanent loads. The section is reinforced with H20 high-bond bars at 200 mm spacing in both the vertical and horizontal directions, with a nominal (clear) cover of 40 mm to the bars. Given that f_yk = 500 MPa, E_s = 200 GPa, fck = 30 MPa, and E_c, eff = 20 GPa.

i. Check whether the reinforcement satisfy the minimum area required for crack control.
ii. Determine the maximum spacing of cracks on the outer face due to the hoop tension.
iii. Determine the maximum crack width on the outer face due to the hoop tension.
iv. Suggest a solution if the maximum crack width exceeds allowable value.

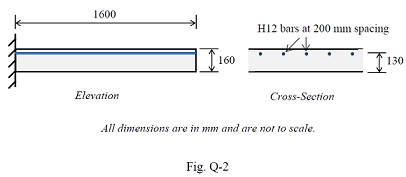
Question 2. The cantilever slab shown in Fig. Q-2 is exposed to the environment (R.H. = 80%) on its underside only. The slab is reinforced with H12 top bars at 200 mm spacing. Bottom bars are not shown and may be ignored.

Determine the maximum long-term deflection of the slab under a quasi-permanent load (inclusive of self-weight) of 15 kN/m2. Include the effect of creep and shrinkage of concrete.

Suggest a solution if the deflection exceeds the limiting value. No calculation is needed.

Given: fck = 30 MPa, fctm = 2.9 MPa, Ecm = 32.8 GPa, fyk = 500 MPa, xu = 82.6 mm, Iu = 363 x 10⁶ mm4/m, xc = 40.1 mm, Ic = 93.8 x 10⁶ mm4/m; Creep coefficient, ?? (∞, t₀) = 1.6, Total shrinkage strain, ?_cs = 250 x 10^-6 mm/mm

The maximum elastic deflection of a cantilever is 1/4 (1/r) l² under uniform load and 1/2 (1/r) l² under an end moment where (1/r) is the maximum section curvature and l is the span.