Reference no: EM132365575

Linear Algebra Questions -

Q1. a) Define what it means for the vectors v₁, . . . , v_n, in a vector space V over a field K to be linearly independent.

b) Define the rank of a matrix.

In the following questions, justify your answers.

c) Compute the rank of the 4(i) x 6(j) matrix B_4,6 whose (i, j) entry is j:

d) For integers m, n ≥ 1, compute the rank of the m x n matrix A_m,n all of whose entries equal 1.

e) Compute the rank of the 5 x 5 matrix A whose (i, j) entry is 5(i - 1) + j:

For each of the following assertions, if the statement is true, then give a proof, if it is false, then give a counterexample. You can cite results from the lectures without proof, but make sure that it is clear what you are using.

Let V be a vector space over a field K and let v₁, v₂, v₃ and u be vectors in V.

f) If v₁, v₂, v₃ are linearly independent, then v₁, v₂, v₃ + v₁ are linearly independent.

g) If v₁, v₂, v₃, u are linearly independent, then v₁, v₂, v₃ are linearly independent.

h) If v₁, v₂, v₃ are linearly independent, then v₁ + v₂ + v₃ might be 0.

i) If v₁, v₂, v₃ are linearly independent, then v₁ - v₂, v₂ - v₃, v₃ - v₁ are linearly independent.

j) If v₁, v₂, v₃ span V, then v₁, v₂, v₃, u also span V.

k) If v₁ = 0, then v₁, v₂, v₃ cannot span V.

l) If v₁ = 0, then v₁, v₂, v₃ cannot be linearly independent.

Q2. a) Show that the eigenvalues of the matrix

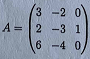
are 1,0, -1, and find the corresponding eigenvectors.

Let V be a vector space over R and let T: V → R³ be a linear transformation. Let v₁, v₂, v₃ ∈ V be three vectors of V and let e₁, e₂, e₃ ∈ R³ be the standard basis vectors. Suppose that

T(v₁) = e₂ - e₃, T(v₂) = -e₁ + e₃, T(v₃) = e₁ - e₂.

b) Show that v₁, v₂ are linearly independent.

c) Find real numbers a₁, a₂, a₃ ∈ R, not all zero, such that a₁v₁ + a₂v₂ + a₃v₃ is in the kernel of T.

d) Suppose also that v₁, v₂, v₃ is a basis of V. Write the matrix of the linear transformation T above with respect to the basis v₁, v₂, v₃ of V and e₁, e₂, e₃ of R³.

Q3. Let n be a positive integer and let A be a square n x n matrix with real entries.

a) Define what are eigenvalues and eigenvectors for the matrix A.

b) Define what it means for the matrix A to be diagonalizable.

Let a, b, c ∈ R be real numbers and let U_a,b,c be the matrix

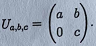
c) Find a choice of a, b, c ∈ R for which the matrix U_a,b,c is invertible. Justify your answer.

d) Find a choice of a, b, c ∈ R for which that the matrix U_a,b,c is diagonalizable and not invertible. Justify your answer.

e) Find a choice of a, b, c ∈ R for which the matrix U_a,b,c is neither diagonalizable nor invertible. Justify your answer.

f) Let C be a 2 x 2 matrix with real entries. Suppose that for every column vector v in R² the two vectors v, Cv are linearly dependent. Show that the matrix C is a multiple of the identity matrix.

Q4. Let A and B be the matrices with real coefficients

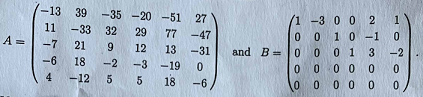
You may use without proof that B is the row reduced form of A.

a) What is the rank of A? Justify your answer.

b) Give a basis for the image of A. Justify your answer.

c) What is the nullity of A? Justify your answer.

d) Give a basis for kernel of A. Justify your answer.

e) Find a row reduced from of the matrix.

Q5. Let R[x]₃ be the real vector space of polynomials of degree at most 3 in the variable x and let T be the function

T : R[x]₃ → R[x]₃

p(x) |→ xp'(x) - p(x).

a) Show that T is a linear transformation.

b) Compute T(1), T(x), T(x²), T(x³).

c) Find the dimension of the image of T.

d) Find a basis for the kernel of T.

e) Does there exist a polynomial of degree 2 not contained in the image of T? Justify your answer.

f) Does there exist a positive integer n such that the rank of Tⁿ is at most 2? Justify your answer.