Reference no: EM132510011

CSCI 6660 Artificial Intelligence - University of New Haven

Question 1. Under Attack

You work for a cybersecurity company, HyperSec, to monitor online forums for fake news. Recently, you've noticed an increasing number of curious sentences that look like this:

"NewHeaven scisetints fnid evenidce taht the erath is falt"

These sentences are perfectly readable by humans, but when you feed them into your machine learning models, they are totally confused and make wildly incorrect predictions. Your automatic fake news detection system is under attack!

a.

As a first s tep, y ou w ould l ike t o c lassify a s entence x a s e ither a dversarial ( y = 1 ) or not (y = -1). Your boss doesn't want you to use the hinge loss because she's worried that the attacker might be able to more easily reverse engineer the system. So you decide to investigate alternative loss functions.

For each of the five loss functions Loss(x, y, w) below:
Determine whether Loss(x, y, w) is usable for classification if we minimize the training loss with stochastic gradient descent (SGD).
• If the answer is yes, compute its gradient ∇_wLoss(x, y, w).
• If the answer is no, explain in one sentence why it is not usable.

(i) Loss(x, y, w) = max {1 - (w.φ(x))y , 0}, where a returns a rounded down to the nearest integer.

(ii) Loss(x, y, w) = max{(w.φ(x))y - 1, 0}.

(iii) Loss(x, y, w) = 1 - 2(w.φ(x))y if (w.φ(x))y ≤ 0
     Loss(x, y, w) = (1 - (w.φ(x))y)² if 0 < (w.φ(x))y ≤ 1
     Loss(x, y, w) = 0 if (w.φ(x))y > 1

(iv) Loss(x, y, w) = max(1 - (w.φ(x)), 0) + 10 if y = +1 .
      Loss(x, y, w) = max(1 + (w.φ(x)), 0) - 10 if y = -1

(v) Loss(x, y, w) = σ( (w φ(x))y), where σ(z) = (1 + e-z)^-1 is the logistic function.

b.
Your next job is to decide which features to use in order to solve the classification problem.
Assume you have a set D of real English words.
(i) Suppose you have a sentence x which is a string; e.g., x = "erath is falt". Write the Python code for taking a sentence x and producing a dict representing the fol- lowing two feature templates:
1. x contains word ___
2. number of words in x that are not in D
Assume that words in x are separated by spaces; e.g., the words in x above are "erath", "is", "falt".

def featureExtractor(x, D): phi = defaultdict(float)

return phi

(ii) If k is the number of unique words that occur in the training set and D is the number of words in the given set of real English words, what is the number of features that the linear classifier will have?

(iii) Suppose that an insider leaks HyperSec's classification strategy to the attackers. The classifier itself was not leaked, just the classification strategy behind it, which reveals that HyperSec is using a dataset of adversarial sentences to train a classifier with the features defined in part (i).

The attackers then use this information to try modifying any fixed sentence (e.g., "climate change is a hoax") into something readable by humans (e.g., "clmaite canhge is a haox") but classified (incorrectly) as non-adversarial by HyperSec. How can the attackers achieve this? Explain the adversarial approach and its steps.

c.
Having built a supervised classifier, you find it extremely hard to collect enough examples of adversarial sentences. On the other hand, you have a lot of non-adversarial text lying around.

(i) Suppose you have a total of 100,000 training examples that consists of 100 adversarial sentences and 99,900 non-adversarial sentences. You train a classifier and get 99.9% accuracy. Is this a good, meaningful result? Explain why or why not.

(ii) You decide to fit a generative model to the non-adversarial t ext, w hich is a distribution p(x) that assigns a probability to each sentence x. For simplicity, let's use a unigram model:

         n
p(x) = ∏p_u(w_i),
         i=1

where w1, w2, ..., wn are the words in sentence x, and pu(w) is a probabilitiy distribution over possible w's.

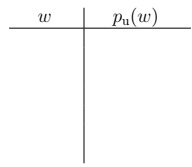
Suppose you are given a single sentence "the cat in the hat" as training data. Com- pute the maximum likelihood estimate of the unigram model pu:

(iv)  Given an unseen sentence, your goal is to be able to predict whether that sentence is adversarial or not. You have a labeled dataset D_train = {(x₁, y₁), . . . , (x_n, y_n) and would like to use the unigram model to train your predictor.

How could you use p(x) (from the previous problem) and train to obtain a predictor f (x) that outputs whether a sentence x is adversarial (y = 1) or not (y = 1)? Be precise in defining f (x). Hint: define a feature vector φ(x).
f (x) =

d.
You notice that the adversarial words are often close to real English words. For example, you might see "erath" or "eatrh" as misspellings of "earth". Furthermore, the actual number of adversarial words is rather small (it seems like the attacker just wants to reinforce the same messages). This makes you think of another unsupervised approach to try.

Let D be the set of real English words as before and a₁, . . . , a_n be the list of adversarial words you've found, and let dist(a, e) be the number of edits to transform some adversarial word a to the English word e (how exactly distance is defined is unimportant).

We wish to choose K English words e₁, . . . , e_K ∈ D and assign each adversarial word ai to one of the chosen English words (z_i ∈ 1, . . . , K ). Each English word e ∈ D incurs a cost c(e) if we choose it as one of the K words. Our goal is to minimize the total cost of choosing e₁, . . . , e_K plus the total number of edits from adversarial words a₁, . . . , a_n to their assigned English words e_z1 , . . . , e_zn.

As an example, let D = "earth", "flat", "scientists" with c("earth") = 1, c("flat") = 1, c("scientists") = 2, and a1 = "erath", a2 = "falt", a3 = "eatrh". Then with K = 2, one possible assignment (presumably the best one) is e₁ = "earth", e₂ = "flat", z₁ = 1, z₂ = 2, z₃ = 1.

(i) Define a loss function that captures the optimization problem above: Loss(e₁, . . . , e_K, z₁, . . . , z_n) =

(ii) Derive an alternating minimization algorithm for optimizing the above objective. We alternate between two steps. In step 1, we optimize z₁, . . . , z_n. Formally write down this update rule as an equation for each zi where 1 ≤ i ≤ n. What is the runtime? You should specify runtime with big-Oh notation in terms of n, K and/or |D|.

(iii) In step 2, we optimize e₁, . . . , e_K. Formally write down this update rule as an equation for each ej where 1 ≤ j ≤ K. What is the runtime? You should specify runtime with big-Oh notation in terms of n, K and/or |D|.

(iv)  Is the above procedure guaranteed to converge to the minimum cost solution? Explain why or why not. If not, what method what algorithm could you use with such guarantees?

2. Maze

One day, you wake up to find yourself in the middle of a corn field holding an axe and a map (Figure 1). The corn field consists of an n n grid of cells, where some adjacent cells are blocked by walls of corn stalks; specifically, for any two adjacent cells (i, j) and (i', j'), let W ((i, j), (i', j')) = 1 if there is a wall between the two cells and 0 otherwise. For example, in Figure 1, W ((1, 1), (1, 2)) = 0 and W ((1, 2), (1, 3)) = 1.

You can either move to an adjacent cell if there's no intervening wall with cost 1, or you can use the axe to cut down a wall with cost c without changing your position. Your axe can be used to break down at most b0 walls, and your goal is to get from your starting point (i0, j0) to the exit at (n, n) with the minimum cost.

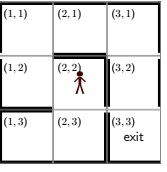
Figure 1: An example of a corn maze. The goal is to go from the initial location (i₀, j₀) = (2, 2) to the exit (n, n) = (3, 3) with the minimum cost.

a.
(i) Fill out the components of the search problem corresponding to the above maze.
• sstart = ((i₀, j₀), b₀).
• Actions(((i, j), b)) = {a ∈ {(-1, 0), (+1, 0), (0, -1), (0, +1)} :
(i, j) + a is in bounds and (W ((i, j), (i, j) + a) = 0 or b > 0)}.
• IsEnd(((i, j), b)) =

• Succ(((i, j), b), a) =

• Cost(((i, j), b), a) =

(ii) When you use an axe to take down a wall, the wall stays down but the set of walls which have been taken down are not tracked in the state. Why does our choice of state still guarantee the minimum cost solution to the problem?

b.
Solving the search problem above is taking forever and you don't want to be stuck in the corn maze all day long. So you decide to use A*.

(i) Define a consistent heuristic function h(((i, j), b)) based on finding the minimum cost path using the relaxed state (i, j) where we assume we have an infinite axe budget and therefore do not need to track it. Show why your choice of h is consistent and what you would precompute so that evaluating any h(((i, j), b)) takes O(1) time and precomputation takes O(n² log n) time.

(ii) Noticing that sometimes h is the true future cost of the original search problem, you wonder when this holds more generally. For what ranges of b0 and c would this hold? Assume for this part that there is a path that doesn't require breaking down any walls.

≤ b0 ≤ c

Your lower bounds need not be tight, but you need to formally justify why they hold.

c.
Having solved the search problem above, you are eager to set out on your journey through the maze, but you realize that breaking down corn stalks is harder than you thought. Suppose that each attempt to break down a wall has an s > 0 probability of failing. Recall that b0 is the maximum number of walls you can break down, not the number of attempts, and each attempt to break down a wall has cost c.

(i) Suppose that each attempt to break down a wall is independent (e.g., if you fail once, the next attempt at the same wall also has probability s of failing regardless of your previous failures). You are interested in minimizing the expected cost of exiting the maze. While the natural solution is to treat this as an MDP, it turns out you can still cast this problem as a search problem. In particular, define a modified Cost(((i, j), b), a) function, and write one sentence about why this choice gives you the optimal policy.

(ii) Suppose instead that each attempt to break down a wall is perfectly de- pendent (e.g., if you fail once, you will always fail to break down that wall). Let us model this problem as an MDP. What should the states of the MDP be? What is the number of states in the worst case as a function of b0 and n (use big-Oh notation)? In this problem suppose b₀ << n.

(iii) If the probability of successfully breaking down a wall is (1 s)/k, where k > 0 is the number of times you've tried to break down a wall. What should the states of the MDP be now?

d.

Let's actually solve the maze! In this specific 3 3 maze as shown in Figure 1, the initial location is (2, 2) and the exit is (3, 3). For simplicity assume that b0 = 1 and that your axe always succeeds (s = 0).

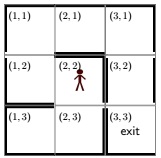
Figure 2: Same corn maze from Figure 1, repeated for convenience.

(i) Compute the minimum achievable cost as a function of c.

(ii) Let's look at the optimal policy at the initial location. For each value of c, what are corresponding optimal actions? If there is a tie between optimal actions state all of them. Your answer should consist of statements of the form: if c ∈, then the optimal actions are .

3. Faulty Accumulator
You decide to try your hand at building hardware. Specifically, you will build a simple circuit that takes n numbers and incrementally computes their sum. However, it turns out hardware is hard, and in your first attempt, the accumulator occasionally gets zeroed out randomly.

To capture this precisely, we can define the following generative model whose Bayesian network is shown in Figure 3. Let Y0 = 0 be the initial sum. For each time step i = 1, . . . , n, the circuit:
1. Receives an input number Xi chosen uniformly from {1, 2, 3, 4}.
2. Decides to remember (Ri = 1) with probability 1 s or forget (Ri = 0) with probability
s.
3. Computes the running sum: Yi = RiYi-1 + Xi, where Yi-1 is added depending on Ri. As an example:
1. X1 = 3, R1 = 1, Y1 = 3 (remember)
2. X2 = 2, R2 = 0, Y2 = 2 (forget)
3. X3 = 4, R3 = 1, Y3 = 6 (remember)
4. X4 = 4, R4 = 1, Y4 = 10 (remember)

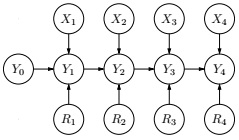
Figure 3: Bayesian network corresponding to the faulty accumulator.

a.
To speed things up, you want to first prune the domains of variables. Recall that when we enforce arc consistency on a variable A with respect to a factor f , we keep a value v in the domain of A if and only if there exist values for other variables in the scope of f such that f evaluates to a non-zero number.

(i) What is the domain of Y_n as a function of n?

(ii) Consider the following factor, where we have marginalized out R₂:
p(y₂ | y₁, x₂) = ∈p(y₂ | y₁, x₂, r₂ = 0) + (1 - s)p(y₂ | y₁, x₂, r₂ = 1). (1)

Suppose Y₁ ∈ {1, 2} and Y₂ = 3. What is the domain of X2 after enforcing arc consistency on X₂?

b.
Now, disregarding what was done during part a, let us explore how conditioning on evidence changes our beliefs about X₂.
(i) Compute:

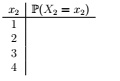
(ii) Suppose we observe that Y₂ = 3. Now what do we believe about X₂?

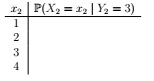
(iii) Suppose we observe Y₂ = 3 and Y₁ = 2. Compute

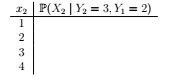
c.
Suppose you wish to compute the posterior distribution over all other variables given Y₁ = 3, Y₂ = 2, Y₃ = 6, Y₄ = 10. You're getting tired of doing probabilistic inference by hand, so you decide to implement Gibbs sampling to do it. Suppose you start out with the following configuration:

(i) Compute the Gibbs sampling update for

P(X₂ | everything else) = P(X₂ | X₁, X₃, X₄, Y_1, . . . , Y₄, R₁, . . . , R₄) = (2)

(ii) Compute the Gibbs sampling update for
P(Y₂ | everything else) = P(Y₂ | X₁, . . . , X_4, Y₁, Y₃, Y₄, R₁, . . . , R₄) = (3)

(iii) What is the problem with running Gibbs sampling on this Bayesian net- work? What alternative would you suggest?

Attachment:- Artificial Intelligence.rar