Reference no: EM132573082

PART 1

Question 1. For each of the following sentences, determine whether or not it is a valid proposition, and why.
If today is Monday, then tomorrow is Sunday.
If today is Christmas Day, then tomorrow is a holiday.
x^(2 )+ 5 =9
They are not studying mathematics
Moscow is the capital of Russia.
14 ÷ 2=24
They are going on holiday.
Find a synonym for the word ‘positive'.
Ernst Sundt is the Rector of Noroff University College.

Question 2. Determine whether each of the following relations is a function on the set {1,2,3,4} . Justify your answers.
f = {(1,2),(1,2),(2,2),(3,2),(4,1)}
f = {(4,1),(3,2),(2,3),(1,4)}
f = {(1,1),(2,2),(3,2)}
f = {(1,1),(2,2),(3,1),(4,2)}
f = {(2,1),(1,2),(3,4),(3,1),(2,3)}

Question 3. Let A = {1,2,3,4,5} . Find the inverse of the following functions f: A → A:
f = {(1,1),(2,3),(3,2),(4,4),(5,5)}
f = {(1,5),(2,4),(3,2),(4,1),(5,4)}
f = {(2,1),(3,4),(1,3),(4,1),(5,2)}

Question 4. Let c be a contradiction. Show that p∨c ≡pby producing an appropriate truth table.

Question 5. Create a truth table to show that ¬(p∧q)∨(¬p∧q)?¬p

Question 6. By using a truth table, determine whether the following proposition is satisfiable (ie, that there is at least one instance in which it can evaluate to True): (¬p∨q)∧(q→¬r∧¬p)∧(p∨r)

Question 7. Let p denote "He is rich" and q denote "He is happy." Write each of the following sentences in symbolic form using p, q and appropriate connectives.
a. If he is rich, then he is unhappy.
b. He is neither rich nor happy.
c. It is necessary to be poor in order to be happy.
d. To be poor is to be unhappy

Question 8. Given the following binary relations R on two sets, for each relation.
Draw the arrow diagram of R.
Is R a function, and why?
If R is a function, determine if it is injective or surjective. Is the function bijective? Justify your answers.
R = {(a,3),(c,1)} on domain {a,b,c} and codomain {1,2,3}
R ={(1,a),(3,c),(2,b)} on domain {1,2,3} and codomain {a,b,c}
R = {(a,b),(b,c),(d,b),(c,c)} on domain {a,b,c,d} and codomain {a,b,c,d}
R = {(a,y),(b,z)} on domain {a,b} and codomain {x,y,z}

Question 9. Suppose A and B are two nonempty sets. Can A×B ever be a functionA→B ?
Explain your answer.

Question 10. Using appropriate laws of equivalence, demonstrate that

¬(p∨¬(r∧¬s))≡¬(p∨s)∧r

Prove your answer using a truth table.

Question 11. Rewrite the following statements without the conditional:
If Sue is a writer, she will be poor.
If it is raining, he uses an umbrella.

Question 12. Consider the proposition "Somebody is older than everybody." Rewrite this proposition in the form "∃ a person x such that ∀___________"

Question 13. Negate the following statements:
a. (∀x∈S) (x+4≤8)
b. (∃x∈A) (x+3<5)
c. ∀x∃y,Q(x,y)
d. ∀x∀y,Q(x,y)
e. ∃y∃x∀z,Q(x,y,z)

Question 14. Write the negation of each of the following propositions:
a. If A is an apple, then A is a fruit.
b. If an integer is divisible by 2, then it is even.
c. If x≥0, then x>0 or x=0.
d. If Sue is Sam's mother, then Ben is her uncle and Abby is her aunt.

Question 15. Rewrite the following propositions in the conditional (if-then) form:
a. Passing all program courses is sufficient condition for being awarded a Bachelor degree.
b. The loop will repeat N times if it does not contain a break or go-to statement
c. A necessary condition for the computer program to be correct is that it does not produce error messages during compilation.
d. A sufficient condition for the Red Sox to win the world championships is that they win all remaining games in the season.

Question 16. Rewrite the statements below in the following form:
∃ ______ x such that ___________
a. Some mammals have four legs.
b. Some real numbers are rational.

Question 17. Rewrite the statements below in the following form:
∀ ______,if _______ then _______
a. Any valid argument with true premises has a true conclusion.
b. The sum of any two odd integers is even.
c. The product of any two odd integers is odd.

Question 18. Use De Morgan's laws to write the negation for this proposition:
"This computer program has a logical error in the first ten lines or it is being run with an incomplete data set."
Show all steps taken to derive your solution.

Question 19. Write the contrapositive, converse and inverse for the following propositions:
a. If p then q.
b. If today is Wednesday, then I have a test today.
c. If n is divisible by 6, then n is divisible by 2 and n is divisible by 3.
d. ∀x∈R,Q(x)→P(x)

Question 20. Use the rule of Modus Tollens to derive the valid conclusion for the argument:
If a computer is correct, then compilation of the program does not produce error messages.
Compilation of this program produces error messages.
Therefore, ________________________.

Question 21. Use the rule of Modus Ponens to derive the valid conclusion for the argument:
All minions love bananas.
Stuart is a minion.
Therefore, ________________________.

Question 22. Let A be a 6×4 matrix, B be a 4×4 matrix, C be a 5×4 matrix and D be a 6×6 matrix. Determine which of the following products are defined and find the size of those that are defined.

AD
AB
DA
BD

Question 23. Let A and B be two matrices, defined asfollows:

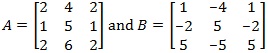
Determine A + B and AB.

Question 24. a.Explain in words the meaning of P (A|B) where Aand Bare twoevents.

b. A survey was conducted at a local magic school. Students were selected at random and asked if they were studying a subject other than Herbology. The results were as follows:

Subject	Potions	Runes	Astronomy	All others	None
Probability	0.26	0.09	0.03	0.03	0.59

What is the probability that a student is studying Potions, given that they are studying some subject otherthanHerbology.

Question 25. Given the proposition ∃x∈R,∀ y∈R (x+y=0)
a. Rewrite this proposition in English without the use of quantifiers.
b. Find the negation of the given proposition.

Question 26. Consider the predicate P(x,y): x=y÷2 with the domain being the collection of non-negative integers (i.e. the numbers 0, 1, 2, 3, ...). What are the truth values of the propositions P(2,4) and P(12,8)?

Question 27. Given the proposition ∃x∈R,∀ y∈R (x+y=0)
a. Rewrite this proposition in English without the use of quantifiers.
b. Find the negation of the given proposition.

Question 28. Let P(x) denote the statement ‘x is a farmer,', and let Q(x) denote the statement ‘x owns a Land Rover.' Rewrite each of the following statements using P and Q and appropriate logic symbols and quantifiers.
For example, the statement "All farmers own Land Rovers" can be re-written as ∀x(P(x)∧Q(x))
Some farmers own a Land Rover.
If the person is a farmer, they will own a Land Rover.
Only one farmer doesn't own a Land Rover.
If someone owns a Land Rover, they might not be a farmer!

Question 29. a. Write the input/output (truth) table for the following circuit:

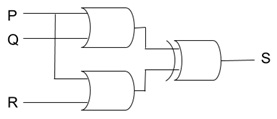
b. What is the output signal S given P=0, Q=1, R=0. (1 mark)

Question 30. Create the input/output table to show the output signal values of R and S for all signal values of P and Q.

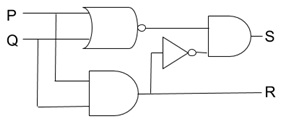
Question 31. A local bar"JuzzBeer" is considering the recent customer ratings posted to TripAdvisor. Let A and B be the events that a customer will award therestaurant a 5 stars or 4 stars rating respectively. Given P (A) = 0.23 and P (B) = 0.42 , find:
P(A ¯)
P(A∪B)
P(A∩B)

Question 32."JuzzBeer" bar recently conducted a survey into the entertainment preferences of their customers. They discovered that 40% enjoy karaoke, 30% like a jukebox, and 10% like both.
What is the probability that a customer likes having a jukebox in the bar if you already know they enjoy karaoke?
What is the conditional probability that a customer who does not like karaokelikes the jukebox?

Question 33. A test for a disease that affects 0.1% of the population is 99% effective on people with the disease. In other words, the test says that the person has the disease with a probability of 0.99. The test gives a false reading (saying that a person who does not have the disease is affected with it) for 2% of the population who do not have the disease. Testing for the disease can be thought of as a two­stage process. In Stage 1, we either choose someone with the disease or we don't. In Stage 2, the test is either positive or it isn't.
Draw a fully labelled probability tree for this process, showing all possible events and probability calculations.
What is the probability that a person selected at random and given a test for the disease tests positive?
What is the probability that someone who tests positive actually has the disease?
Consider the results of your analysis of this data. What does this tell us about the reliability of this test? (i.e., what does this result mean?)

PART 2

Question 1. Enumerate (i.e. list) the members of the following sets:
a. {x is a positive integer less than 12}
b. {x is the square of an integer and x≤50}
c. {x is an integer such that x^2≤4}

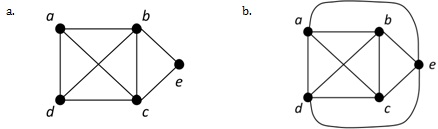
Question 2. Draw the graph with the adjacency matrix:

a.

b.

Question 3. Suppose that d1,d2,... dnare the degrees of the vertices of a graph G, ordered such that d1≥d2 ≥ ...≥dn. The sequence d1,d2,... dnis called the degree sequence of G.

a.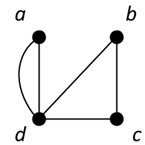

b.

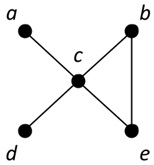
c.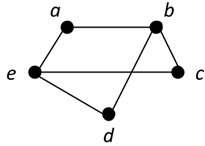

Find the degree sequence of the following graphs:

Question 4. Determine whether each of the following eight statements are True or False. For each answer, explain your reasoning.
a. {y}∈{y}
b. {x}∈{{x}}
c. ∅⊆{x}
d. Q⊂Z
e. Z⊂R
f. Z^+∪Z^+=Z
g. Z∪Q=Q
h.Q∩R=Q

Question 5. Are the following sets equal?
A={x∈Z:5≤x<10} and B={9,8,7,6}, where Z denotes the set of all integers.
Justify your answer.

Question 6. For the following graphs, either find an Euler cycle, or explain why one does notexist.

Question 7. The operator * is defined as follows: A*B=¬(A∩B)
a. Draw a Venn Diagram to illustrate this operator.
b. If A = {1, 2, 3, 4, 5} and B = {3, 4, 5, 6, 7} and U is the set of all positive integers less than 10, draw a Venn diagram to derive A*B.
c. If A=N and B=Z and U=A∪B, what is A*B?

Question 8. First year students studying the online Business Information Studies program can choose which courses to study from a selection of options. Last year, 25 chose to study the Financial Accounting course, 27 chose International Business, and 12 chose Marketing. There were 20 students who took both Financial Accounting and International Business, 5 who opted for Financial Accounting and Marketing, and 3 who studied Marketing and International Business. No students took all three options.

a. Draw a Venn Diagram to illustrate this operator.
b. How many students studied only the Marketing course?

Question 9. A survey was conducted into the number of smartphones sold during the past month by local company ‘The Mobile Warehouse' to local small business customers. The survey concentrated on the latest iPhone (I), the Galaxy Note (N) and Moto G (G) sold to 26 small business customers. The survey results were as follows:
17 purchased iPhones (I)
12 purchased the Galaxy Note (N)
11 purchased the Moto G (G)
6 purchased both I and G
7 purchased both I and N
5 purchased both N and G
2 purchased all three smartphones.

Create a fully labelled Venn diagram of this data, and find the number of companies who purchased:
a. only iPhones
b. only the Galaxy Note
c. only the Mogo G
d. Galaxy Note and Moto G, but not iPhones
e. iPhones and Galaxy Note, but not Moto G
f. only one type of smartphone
g. at least one type of smartphone
h. none of these smartphones
 
Question 10.Consider the following subsets of a standard English language dictionary:
A={x|x is a word that appears before dog}
B={x|x is a word that appears after cat}
C={x|x is a word containing two identical consecutive letters}

Determine the truth value of the following statements. Justify each answer.
a. C⊂A∪B
b. kangaroo∈(¬B)∩C
c. A∩B=∅

Determine the truth value of the following. Justify your answer.
d. moose∈B?C

Describe in words the elements of the following sets.
e. A∩B∩C
f. (A∪B)∩(¬C)

Question 11. Let A={1,2,3,4}. Define the relation R on A by xRy if x≥y.
a. List all members of R.
b. Draw the digraph representing R.
c. Represent R on a cartesian plane.
d. Represent R in a connection matrix.
e. Determine if R is an equivalence relation. Justify your answer.

Question 12. Let A = {1,2,3,4,5} and R be a relation on A where R = {(1,1),(2,2),(3,3), (4,4),(5,5),(1,5),(5,1),(3,5),(5,3),(1,3),(3,1)}
a. Represent R as a connection matrix.
b. Show that R is an equivalence relation on A.
c. List all equivalence classes of R.
d. Derive R^(-1).
e. Let S be a relation on set A, such that S = {(1,2),(2,3),(4,5)}.
Derive R^(-1) o S.

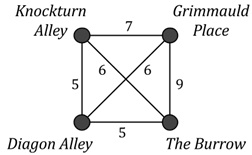
Question 13. a. In your own words, explain what is meant by the Travelling Salesman Problem.
b. Solve the Travelling Salesman Problem for thefollowinggraph.

Question 14. Construct a binary search tree for the sentence "On second thought let's not go to Camelot, it is a silly place." Your tree should use alphabetic ordering during its construction.

Question 15.Let A={a,b,c}, B={x,y} , C={0,1} and U={a,b,c,x,y,z,0,1,T,F}. Find the following:
a. A∪C
b. A∪B ¯
c. (A∩B) ¯
d. AΔB
e. P(C∪B), where P(x) represents the powerset of x.
f. A×B
g. B×C
h. A×B×C
i. B×A×C
j. What is |P(B×A×C)|?

Question 16. Let A be the set of English words that contain the letter a, and let B be the set of English words that contain the letter b. Express each of the following sets as a combination of A and B:
a. The set of English words that do not contain the letter a.
b. The set of English words that contain either an a or a b.
c. The set of English words that contain both an a and a b.
d. The set of English words that contain an a but not a b.

Question 17. Create a Huffman compression code for the phrase "Hufflepuff House"(ignoring character case). You answer should include your Huffman code tree (including clear illustration of it's development) plus the resultant encodedphrase.

Question 18. Alice has decided that the Mad Hatter is not very good at hosting tea parties. None of his acquaintances get along with all of the others, so whenever he tries to gather them around for a warm beverage it always ends in arguments and upset. Alice has therefore decided he needs to get organized! In order to show him that with a little thought (and logic) he can host a successful tea party she has invited everyone around next Friday evening. To make sure the party is successful, Alice decides to create a seating plan. The challenge in creating this seating plan is that each guest has a number of adversaries to whom they must not be seated!

The guests, along with corresponding list of adversaries, are asfollows:
Alice ­ Cheshire Cat, Duchess, Gryphon
Cheshire Cat ­ Alice, Dormouse, White Rabbit
Dormouse ­ Cheshire Cat, Mad Hatter, White Rabbit
Duchess ­ Alice, Gryphon, March Hare
Gryphon ­ Alice, Duchess, Mad Hatter
Mad Hatter ­ Dormouse, Gryphon, March Hare March
Hare ­ Duchess, Mad Hatter, White Rabbit White
Rabbit ­ Cheshire Cat, Dormouse, March Hare

Draw the graph representing these eight guests and their friends, and find a seating arrangement where each person sits between two friends (i.e., no­one sits next to one of their adversaries).

Question 19. During Alice's tea party, some of the guests decide to hold a round­robin chess tournament throughout the following week. By the end of that week the following games have been played: Alice beat the Cheshire Cat, the Cheshire Cat beat the Gryphon, the March Hare beat the Cheshire Cat, Alice beat the Gryphon, the March Hare beat Alice, the March Hare beat the Gryphon, the Cheshire Cat beat the White Rabbit, Alice beat the White Rabbit, the White Rabbit beat the Gryphon, and finally the March Hare beat the White Rabbit.
Model this outcome with a directed graph. By finding the in­degree andout­degreeof each vertex, determine who was the final winner of the tournament.

Question 20. Alice has found a map showing all safe routes between a number of locations in the local area, represented as a graph:

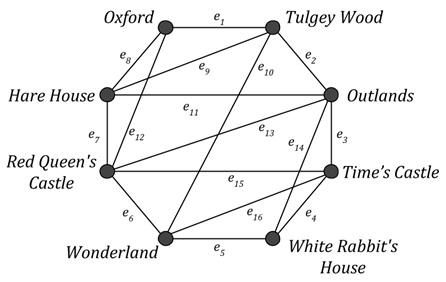
Create the adjacency matrix for this graph, based on an appropriate ordering of the vertex set V.

Hint: This may be easier if you re­label your vertices, for example:

a	Oxford	e	Tulgey Wood
b	Hare House	f	Outlands
c	Red Queen's Castle	g	Time's Castle
d	Wonderland	h	White Rabbit's House

How many paths of length 4 exist from vertex n to vertex m in the above graph, where n and m are any two vertices inV?

Alice is currently in Oxford and wants to get to the White Rabbit's House. Given the following additional data about the distance between each location, use Dijkstra's algorithm to find the shortest path from Oxford to the White Rabbit's House. When answering this question you must show every step in your calculations, including your final fully­labelled graph.

edge	distance	edge	distance	edge	distance	edge	distance
e1	6	e5	4	e9	2	e13	3
e2	3	e6	3	e10	3	e14	5
e3	3	e7	4	e11	3	e15	5
e4	2	e8	4	e12	5	e16	1

Question 21. Before leaving Wonderland, Alice wishes to take her friend Dinah on a tour of the most interesting places she has recently visited. However, having decided that the local residents are rather strange, they wish to meet with the least number of characters possible during this final exploration. Using the following map (from question 8) with the additional information about how many characters they would meet along each road (edge), use Prim's Algorithm to find the minimum spanning tree where Alice and Dinah will have the fewest number of encounters whilst visiting each location (vertex).

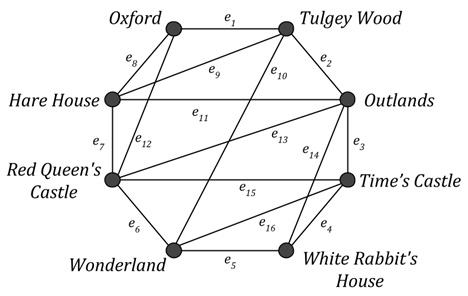
edge	characters	edge	characters	edge	characters	edge	characters
e1	3	e5	7	e9	8	e13	2
e2	4	e6	6	e10	6	e14	4
e3	6	e7	5	e11	3	e15	8
e4	2	e8	3	e12	4	e16	1

When answering this question you must show every step in your determination of the spanning tree, including your final minimum spanning tree and total weight (i.e., minimum possible number of encounters with local characters). In order to simplify the process you may wish to re­label the vertices in the above graph according to the suggestion in question 20.

PART 3

In your own words, discuss the possible uses of the topics covered in this subject in the real world (Use minimum 500 words in total).

Why do you think studying Discrete Mathematics is relevant for a person that wishes to pursue a career in your chosen discipline?

What aspects of this subject did you find very relevant/ or not relevant to yourself?

What can you do to further improve your understanding of the subject matter in future?