Reference no: EM132472603

MATH 240 MATLAB Project Assignment -

For this project, do all problems in format short. Review all directions and rules. Then enter the command clock.

1. Let A = .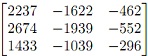

(a) Execute the command [P, D] = eig(A) to diagonalize A.

(b) Use MATLAB to verify that A = PDP^-1.

(c) Use the previous results to give the eigenvalues of A, and give an eigenvector for each eigenvalue.

2. Let A = .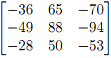

(a) Use MATLAB to compute Aⁿ for n = 2, 3, 4, 5, 6, 7, 8. Do you notice a pattern?

(b) Have MATLAB produce an invertible P and a diagonal D such that A = PDP^-1. Notice that complex numbers get involved.

(c) To understand Aⁿ, it suffices to understand Dⁿ because Aⁿ = PDⁿP^-1. Describe the pattern that emerges when we consider powers of D: D, D², D³, D⁴, etc.

(d) Without doing a computation in MATLAB, determine A^20000001.

3. Let A =.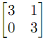

(a) Execute the command [P, D] = eig(A). Something strange should occur in the output.

(b) Use MATLAB to try see if A = PDP^-1.

(c) Find a basis for the eigenspace of A corresponding to the eigenvalue λ = 3.

(d) Is there a basis for R² consisting of eigenvectors for A? Does this explain why something went wrong in part (b)?

4. Let A = .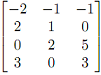

(a) Enter A into MATLAB and use MATLAB to compute the dot product of the first column of A with its second column. Also compute the dot product of the third column with itself.

(b) Compute the matrix product A^TA.

(c) What is the relationship between the entries of A^TA and the dot products of the columns of A? Make sure your answer is consistent with your computations.

(d) What in general is the relationship between the entries of AA^T and dot products of vectors associated to A?

(e) Compute AA^T and do at least two dot product computations to support your previous answer.

(f) Let Q = 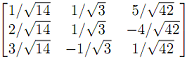. Do a single matrix computation which shows that the columns of form an orthonormal set.

(g) Explain carefully why your computation above shows that the columns form an orthonormal set.

(h) Explain why the rows of Q must also form an orthonormal set.

5. Let W be the subspace of R⁵ given by

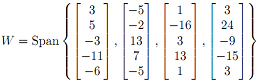
(a) Enter the four vectors into MATLAB as v1, v2, v3 and v4 respectively.

(b) Let A = [v1 v2 v3 v4]. Compute the rank of this matrix. Explain briefly in a comment why this shows that this set of four vectors is a basis for W.

(c) We shall apply the Gram-Schmidt Process to produce an orthogonal basis {w₁, w₂, w₃, w₄} for W. To begin, let w1 = v1 and w2 = v2 - (dot(w1,v2)/dot(w1,w1))*w1.

(d) Continue the Gram-Schmidt Process and compute w3 and w4.

(e) Rescale each vector of the orthogonal basis {w1, w2, w3, w4} to produce an orthonormal basis {u1, u2, u3, u4} for W. (Recall there is a command in MATLAB to compute the norm of a vector.)

(f) Enter the vectors u1, u2, u3, u4 into the columns of a matrix Q. Verify that the columns of Q are orthonormal with a single matrix multiplication.

(g) Compute R = Q^TA. Verify that R is upper triangular with positive diagonal entries and that A = QR.

(h) MATLAB can compute a QR factorization in a single command. Enter [Q1, R1] = qr(A, 0). Notice that there is a small discrepancy between your Q, R and the Q1, R1 produced by MATLAB. This is because QR factorizations are not unique. They are only unique if we insist that the diagonal entries of R are all postive. Nonetheless, the columns of Q1 still form an orthonormal basis for W.

6. Let W be the subspace of R⁶ given by

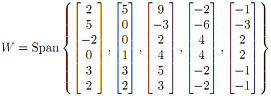
(a) Enter those five vectors as the columns of a matrix A and compute its rank.

(b) The previous computation shows that the five vectors are linearly dependent, hence they do not form a basis for W. Find a basis for W. (Hint: Treat W as Col A).

(c) Enter your basis for W as the columns of a matrix B. Compute the factorization B = QR with a single command. Give an orthonormal basis for W.

(d) Let E = QQ^T. As a linear transformation on R⁶, E is the orthogonal projection onto the subspace W. Use E to compute the orthogonal projection of the vector v = (1, 1, 1, 1, 1, 1)^T onto W.

(e) Find a basis for W^⊥ as follows. Note that W = Col A = Col B. From a theorem in class, we have

W^⊥ = (Col B) ^⊥ = Nul(B^T),

so it suffices to find a basis for Nul(B^T).

(f) As you did for W, find an orthonormal basis for W^⊥.

(g) Compute the matrix F for the orthogonal projection onto W^⊥. What is the sum E + F?

Attachment:- Matlab Project Assignment File.rar