Reference no: EM132231396

Introduction to Financial Mathematics Assignment -

Let W = (W_t)_t≥0 be a standard Brownian motion.

1. As we've seen, the Ito integral is defined by sampling the integrand b = (b_t) at the left endpoints of each subinterval,

₀∫^Tb_tdW_t =lim_{n→∞ k=1}Σⁿb_(k-1)Δt(W_kΔt - W_(k-1)Δt), (1)

where Δt = Δt(n) = T/n. Using the left endpoints was a choice, and in this exercise we will explore the implications of choosing other points, including the right endpoints and all points in between. We will focus on perhaps the simplest non-trivial stochastic integral, ₀∫^TW_tdW_t. To this end, define for p ∈ [0, 1] the p-stochastic integral

I_p(₀∫^TW_tdW_t) = lim_{n→∞ k=1}ΣⁿW_(k-1+p)Δt(W_kΔt - W_(k-1)Δt), (2)

where Δt = Δt(n) = T/n. Observe that p = 0 corresponds to using the left endpoints, as we do in the Ito integral. In contrast, p = 1 corresponds to using the right endpoints, and p = ½ corresponds to using the midpoints (the so-called Stratonovich integral). We will prove the following formula,

I_p(₀∫^TW_tdW_t) = ½W²_T - T/2(1-2p), (3)

which demonstrates that the choice of p is critical to the calculation of the p-stochastic integral. Again, if the Riemann integral were sufficient, then the choice of p would not matter in the result.

Much of the analysis will be very similar to the calculation of ₀∫^TW_tdW_t as an Ito integral in the notes on stochastic integration.

(a) Show that

_k=1ΣⁿW_(k-1+p)Δt(W_kΔt - W_(k-1)Δt) = A + B + C, (4)

where

A = _k=1ΣⁿW_(k-1)Δt(W_kΔt - W_(k-1)Δt) (5)

B = _k=1Σⁿ(W_(k-1+p)Δt - W_(k-1)Δt)(W_kΔt - W_(k-1+p)Δt) (6)

C = _k=1Σⁿ(W_(k-1+P)Δt - W_(k-1)Δt)² (7)

(b) Observe that lim_n→∞ A is just the Ito integral, which we calculated in the notes. Retrieve its value:

lim_n→∞ A = (8)

(c) Use properties of the Brownian motion to show that

(W_(k-1+p)Δt - W_(k-1)Δt) (W_kΔt - W_(k-1+p)Δt) 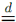Δt√(p(1-p))Z_kZ^⊥_k (9)

where Z_k and Z_k^⊥ each have a standard normal distribution and Z_k and Z_k^⊥ are independent. (The symbol 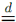means "has the same distribution as.") Use this and the law of large numbers to argue that lim_n→∞ B = 0.

(d) Use properties of the Brownian motion to show that

W_(k-1+p)Δt - W_(k-1)Δt 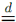 √(pΔt)Z_k, (10)

where Z_k has a standard normal distribution. Use this and the law of large numbers to argue that lim_n→∞ C = pT.

(e) Combining the above, show the formula (3) holds.

(f) For which value of p does follow the classical rules of calculus, i.e. I_p(₀∫^TW_tdW_t) = ½W²_T?

2. For fixed T > 0, the stochastic integral ₀∫^Tb_tdW_t is a random variable. As such, we are naturally interested in computing its moments. In this exercise, we will compute expectations for a certain class of stochastic integrals, namely

E[₀∫^Tf(W_t)dW_t] (11)

for an arbitrary but bounded function f : R → R. We wonder if there's a pattern, and if so, whether it depends on f. We have

₀∫^Tf(W_t)dW_t = lim_n→∞ Fn, (12)

where

Fn = _k=1Σⁿf(W_(k-1)Δt) (W_kΔt - W_(k-1)Δt) (13)

and Δt = Δt(n) = T/n.

(a) Find E[F_n] for each n. You may freely use the following fact about independence of random variables: if X is independent of Y, then f(X) is independent of g(Y ) where f, g : R → R are functions.

(b) Let M > 0 be the bound of f, i.e. |f(x)| ≤ M for all x ∈ R. Show that

|F_n| ≤ _k=1ΣⁿM|W_kΔt - W_(k-1)Δt| (14)

Compute the expectation of the right hand side, thereby showing that it is finite. (Hint: You may freely use the following fact: if Z is a standard normal random variable, then E[|Z|] = √(2/π).)

(c) We have

E[₀∫^Tf(W_t)dW_t] = E[lim_n→∞ Fn] = lim_n→∞E[F_n] (15)

where the interchange of the expectation operator and the limit in the second equality is due to the result in (b), which lets us use the dominated convergence theorem. Use the result from (a) on E[F_n] to find the limit and thereby find the expected value. Does it depend on f?

Textbook - The Mathematics of Financial Derivatives : A Student Introduction. Author: Paul Wilmott, Sam Howison, Jeff Dewynne.

Attachment:- Assignment File.rar