Band structure and band occupancy

Reference no: EM131763

QUESTION 1: Band Structure

Carriers in a two-dimensional (2D) sample occupy a conduction band with the approximate energy-wavevector relation

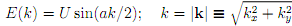
165_Band Structure.png

where a = 2nm is the spacing of the 2D square-lattice "crystal" in real space, and U = 150meV is the maximum spread of the band.

(a) Choose k_y = 0 and roughly sketch E(k) as a function of wavenumber k along the kx-direction. Show the boundary points of the Brillouin zone(BZ).

The complete BZ in 2D is a square centred on k = 0. Draw another sketch, this time of the contour in the 2D zone for which E(k) = U/2. What is the magnitude of k on this contour?

(b) Using Eq. (1), show that the group velocity in the band (still along the x-axis), de?ned as

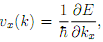
2162_Band Structure1.png

can be written as

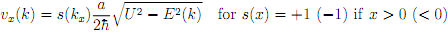
193_Band Structure2.png

(d) The effective mass depends only on k since the band is circularly symmetric, and is given simply by

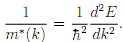
895_Band Structure3.png

Find the expression for the ratio m∗ (k)/me if Eq. (1) holds. How does this ratio behave at the centre of the BZ? Give its value at k = π/a. Explain how the sign of m∗ relates to the band shape there.

QUESTION 2: Band Occupancy

The density of states (DOS), for a sample of 2D material, counts up how many states become available in the band as we move up along its energy curve E = E(k). Its formula in 2D, including spin degenracy of the band, is

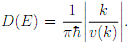
(a) For the same band as in Question 1, sketch D(E) in the range 0 < E < U. What are its units?

(b) When E << U we can approximate the DOS as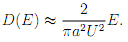

Suppose we are at zero temperature and the band continas electrons with Fermi energy EF; their distribution function (the probability to occupy a state at some given energy) is f(E) = Θ(EF - E) - that is, f = 1 below the Fermi level, and is zero otherwise.

Assuming EF << U, how would you use the information for D(E) from Eq. (3) together with the distribution f(E) to calculate the total number of electrons per cm2 of sample?

(c) Now estimate the density for E_F = 35meV, using the parameter values a and U given in Q.1. On average, how many electrons occupy a unit cell of size a2 in the real lattice?

(d) It turns out that the integration for carrier density over the full DOS can be done exactly up to E = U. It is given by where sin^-1 (x) denotes the sine-inverse function (known in the U.S. as arcsin(x), this ex- pression is NOT the reciprocal 1/ sin(x); it is that value y which satis?es sin(y) = x).

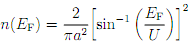
What is the number of electrons per unit cell of the real lattice when E_F = U and also when E_F = U/√2?

Reference no: EM131763

Questions Cloud

Estimate the demand function : Estimate the demand function

Production possibility frontier : Show the country's production possibility curve.

Determine the monthly payment : Investigate the cost of a home mortgage and to determine the monthly payment.

Capital budgeting case : Capital Budgeting Case

Band structure and band occupancy : Find the Band Structure and Band Occupancy

Prepare a partial income statement : The company mostly sells on a retail basis to household consumers, but occasionally receives large orders for tables and chairs from schools and businesses.

Construct a truth table for the boolean expression : Construct a truth table for the Boolean expressions ABC + A'B'C' ABC + AB'C' + A'B'C' A(BC' + B'C)

Statistics test paper : Answer the following three questions based on what you know about statistics now.

How would investors and management view eva and fcf? : How would investors and management view EVA and FCF? Try one that you are familiar with-you shop at their store, eat at their restaurants, or wear their clothes. On their Web site, try to find their annual financial report.

User Account

All Pages