Solving Word Problems Involving Quadratic Equations:

Many algebraic word problems involve quadratic equations. The algebraic expressions any time describing the relationships in the problem involve a quantity multiplied by it; a quadratic equation must be used to solve the problem. The steps for solving word problems involving quadratic equations are the same as for solving word problems involving linear equations.

Example:

A radiation control point is set up near a solid waste disposal facility.  The pad on that the facility is set up measures 20 feet by 30 feet. If a health physicist sets up a controlled walkway around the pad that reduces the area by 264 square feet, how huge is the walkway?

Solution:

Step 1. Let x = Width of the Walkway

Step 2. Then,

30 - 2x = Length of Reduced Pad

20 - 2x = Width of Reduced Pad

Step 3. Area of Reduced Pad =          (Length  of  Reduced  Pad)(Width  of  Reduced Pad)

600 - 264 = (30 - 2x)(20 - 2x)

336 =600 - 100x + 4x²

Step 4. Solve this quadratic equation.

4x² - 100x + 264 = 0

By using the Quadratic Formula, substitute the coefficients for a, b, and c and solve for x.

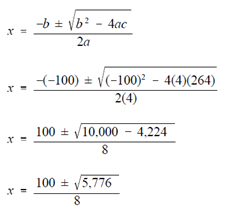
X = 100 ± 76 /8

X = 100+ 76/8, 100- 76 /8

X = 176/8, 24/8

X = 22, 3

The two roots are x = 22 feet and x = 3 feet.   Here x = 22 feet is not physically useful, the answer is x = 3 feet.

Step 5. Check the answer.

The area of the decreased area pad is 264 square feet less than the area of the original pad.

600 - 264 = (20 - 2x)(30 - 2x)

336 =   [20 - 2(3)][30 - 2(3)]

336 = (20 - 6)(30 - 6)

336 =   (14)(24)

336 =   336

Therefore, the answer checks.