Application of Chaotic Sequences

In the subsequent section, the meaning of applying chaotic sequence generator in velocity updation has been described. The random function utilized in Eq. 15 has been replaced along with chaotic function since of the stochastic and ergodic property of the chaotic systems. The cause of utilizing chaotic sequences in place of random number generators is the limitations attached along with the random numbers. Their limitations is one of as: the solution get sealed via sequential co-relation of successive cells via random number generators, thus, this needs more number of generations to converge towards near optimal or optimal solution. Other limitations are such the commonly utilized random number generators contain a tendency to generate the higher order bit more random than their lower order bit counterpart. Hence, there arises require to contain a consistent random number generator that can explore search space without being biased. Currently, different chaotic sequences have been applied in the regions concerned to secure transmission, natural phenomena modeling, neural networks, DNA computing process, and non-linear circuits and encouraging results have been acquired over random number generators. The un-predictability characteristics that are spread spectrum characteristics validate theoretically the employ of chaotic sequence. Hence, the current research drift has been towards the implementation of chaotic sequence generators in different artificial intelligence tools. Such unison gives the fast convergence and also ensure near optimal solutions through establishing a proper balance between exploitation and exploration.

Three various chaotic functions have been utilized as they possess the capability to generate several neighborhoods of near optimal solution for preserving the solution variation and preventing the pre-mature convergence of the search space.

The first one is a Logistic map such can be formulated as given:

                                H_{k + 1} = f (μ, H _k ) = μ . H k (1 - H _k )...............................Eqn(17)

Here

 H_k  ∈ (0, 1), k = 0, 1, ... , n

 Here, H_k is the value of the chaotic variable in k^th iteration,

 μ is a bifurcation parameter of the system.

A graphical presentation of one-dimensional logistic chaotic function is demonstrated in diagram shown below. For 300 generations this graph has been plotted. From the intensive experimentation, this is found that this performs well while H₀ = 0.1 and μ = 3.99.

This can be visualized from diagram shown below in which the spread spectrum characteristic of logistic map explores approximately all search space. Such property enables it to be employed in place of random numbers. The second function generated also from logistic mapping is tent function such can be formulated as shown below:

                                                    H_{k + 1} = G (k ).............................Eqn(18)

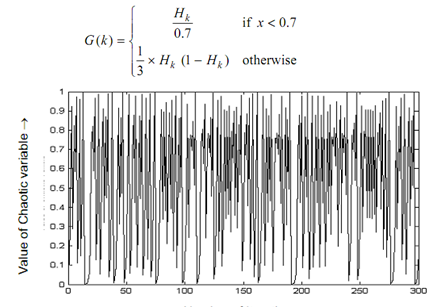
                                     Figure: Chaotic Graph of Logistic Mapping

The third function that can be considered is the sinusoidal iterator defined as

 H_{k + 1} = a . H²_k sin (Π H_k ) . ......... . eq20

 k = 0, 1, 2, . . . n

 This mapping model is iterated along with a = 2.3 and H₀ = 0.7.

The given section explains the significance of Time Varying Acceleration Coefficients or TVAC.