AIS In Data Analysis's Application

The implementation of artificial immune systems in Data analysis model will consist of a set of cells, named antibodies, interconnected by associations along with linked connection strengths. The antibodies are assumed to shown the network internal images of the pathogens as input patterns contained in the environment to such this is exposed. The connections among the antibodies will find out their interrelations, giving a degree of similarity as in a described metric space in between them: the closer the antibodies, the more related as they are. The customized artificial immune network model can be formally explained as:

Definition

The Artificial immune systems based data analysis is an edge-weighted graph, not essentially fully liked, composed of a set of nodes, termed as antibodies, and sets of node pairs termed as edges along with an allocate number named as weight, or connection strength, connected with each connected edge.

The Artificial immune systems based data analysis clusters will serve as like internal images or mirrors causes for mapping existing clusters in the data set into network clusters. Because an illustration, assume there is a data set composed of three regions along with high density of data. The hypothetical network architecture will be produced by the learning algorithm.

The numbers inside the cells showing their labels or the sum of number is usually higher than the number of clusters and much smaller than the number of samples, and the numbers next to the connections represent their strengths, and dashed lines suggest connections to be pruned, in order to detect clusters and define the final network structure.

Notice the presence of three distinct clusters of antibodies, each of which with different number of antibodies, strengths and connections. These clusters map those of the original data set. Notice also that the number of antibodies in the network is much smaller than the number of data samples, differentiate the architecture proper for data compression. At last, the shape of the spatial antibodie's distribution follows the antigenic spatial distribution's shape.

There is no differentiating between the network surface molecules antibodies and their cells. The Ag - Ab and Ab - Ab interactions are quantified via proximity or similarity measures. The goal is to employ a distance metric to generate an antibody repertoire such constitutes the internal image of the antigens to be identified, and evaluate the similarity degree among the artificial immune systems based data analysis antibodies, such as the cardinality of repertoire could be controlled. Hence, the Ag - Ab affinity is inversely proportional to distance among them: the higher the affinity, the smaller the distance and vice-versa.

It is significant to stress such, in the biological immune system or IS, recognition happens throughout a complementary match among a specified antigen and the antibody. Nonetheless, in some artificial immune system applications, and for the intentions of this model, the creation of an antibody repertoire along with similar characteristics as instead of complementary to the antigen set is an appropriate alternative.

Because proposed in the original immune network theory or INT, the existing cells will contend for antigenic recognition and those successful will show the way to the network activation and cell proliferation, whereas those who fail will be removing. In addition, Ab - Ab recognition will conclude in network suppression. In our model, suppression is performed by removing the self-recognizing antibodies, specified a suppression threshold σs. Each pair Ab_j - Ab_{i, j}= 1, . . . M, i = 1, . . . , N, will concern to each other inside the shape-space S via the affinity d_ij of their interactions, that reflects the possibility of starting a clonal

The given notation will be adopted as:

• Ab : accessible antibody repertoire ( Ab ∈ S ^{N × L} , Ab = Ab_{{d }} ∪ Ab_{m} ) ;
• Ab_{m} : whole memory antibody repertoire ( Ab ∈ S ^{m × L} , m ≤ N ) ;
• Ab_{d} : d new antibodies to be placed in Ab ( Ab_{{d }} ∈ S ^{d × L} ) ;
• Ag : antigen's population ( Ag ∈ S ^{M × L} ) ;
• f_j : vector having the affinity of all the antibodies Ab_i (i = 1, . . , , N) along with relation to antigen Ag_j. So affinity is inversely proportional to the Ag - Ab distance;
• S: similarity matrix in between all pairs Ab_i - Ab_j, via elements s_ij (i, j = 1, . . . , N);

  • C: population of Nc clones produced from Ab (C ∈ S ^{Nc  × L} ) ;

 • C*: population C after the affinity maturation process;

• d_j : vector containing the affinity among every element from the set C*along with Ag_j;
• ξ : percentage of the mature antibodies to be chosen;
• M_j : memory clone for antigen Ag_j (stay from the process of clonal suppression);
• *M_j : for antigen Ag_j resultant clonal memory;
• σ_d : natural death threshold;
• σ_s : suppression threshold.

The artificial immune system or IS based data analysis learning algorithm intends at building a memory set that represents and recognizes the data structural organization. The more exact the antibodies, the less parsimonious the network or low compression rate, even as the more generalist the antibodies, the extra parsimonious the network with relative to the number of antibodies to enhanced compression rate. The suppression threshold (σ_s) controls or manages the antibody's clustering accuracy, specificity level and the network plasticity. The Artificial immune systems based data analysis learning algorithm can be illustrate in Programme no.2.

1. At iteration, do:

1.1 For each antigenic pattern

 Ag _j , j = 1, ... , M , ( Ag _j ∈ Ag )

1.1.1 Find out its affinity f_ij, i = 1,...N, to all Ab_i - f_u =1/D_ij

D_ij = ¦¦ Ab_i - Ab_j ¦¦,i = 1,...............N

1.1.2 A subset Ab_{n} composed of the n highest affinity antibodies is chosen;

1.1.3 The n chosen antibodies are going to proliferate or clone proportionally to their antigenic affinity f_i,j, producing a set C of clones : the higher or upper affinity, the larger the clone size for all of the n chosen antibodies.

1.1.4 The set C is submitted to a directed affinity maturation procedure or guided mutation producing a mutated set C*, where all antibody k from C* will suffer a mutation along with a rate α_ks inversely proportional to the antigenic affinity f_i,j of its parent antibody : the higher affinity, the smaller mutation rate:

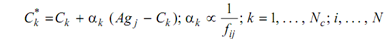
1.1.5 find out the affinity d_kj= 1/D_kj among Agj and each elements of

C* : D_kj  || C*  - Ag_j  ||, k = 1, . . . , N_c .

1.1.6 From C*, re-select ζ% of the antibodies along with highest d_kj and put them keen on a matrix M_j of clonal memory.

1.1.7 Apoptosis: remove all the memory clones from M_j whose affinity D_kj > σ_d.

1.1.8 Find out the affinity S_ik among the memory clones as:

S_ik  = || M_j,i  - M_j,k  ||, ∀ i, k .

1.1.9 Clonal suppression: remove those memory clones that S_ik < σ_s.

1.1.10 Concatenate the whole antibody memory matrix along with the resultant clonal  memory

M_j* for Ab_{m} ←[Ab_{m}; M_j*].

            1.2 finds out the affinity in between all the memory antibodies from

Ab_{m} : S_ik = || Ab_{m} - Ab_{m} ||, ∀ i, k .

 1.3 Network suppression: remove all the antibodies such that S_ik < σ_s.

 1.4 Build the whole antibody matrix

 Ab_{m} ← [ Ab_(m) ; Ab_{d } ] .

                                 Programme no.2: Artificial immune systems Based Data Analysis Learning Algorithm