Maximum Power Transfer Theorem
In an electric circuit, the load accepts electric energy through the supply sources and transforms that energy into a helpful form. The maximum acceptable power accepts by the load is always limited either by the heating effect (in situation of resistive load) or by the other power conversion occurring in the load. The Thevenin and Norton models entail that the internal circuits inside the source will essentially dissipate some of power produced by the source. A logical question will occur in mind, how much power can be transferred to the load from the source under most practical situations? In another words, what is the value of load resistance which will absorbs the utmost power from the source? This is a significant issue in most practical problems and it is explained with an appropriate illustration.
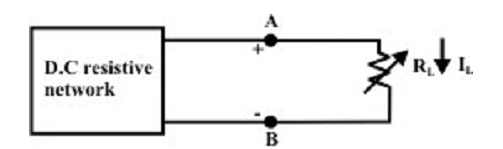
Let us consider an electric network as shown in figure above, the difficulty is to find the selection of the resistance RL and hence the network delivers maximum power to the load or in another words what value of load resistance RL will absorb the maximum quantity of power from the network. This trouble can be resolved by using nodal or mesh current analysis to acquire an expression for the power absorbed by RL, and then the derivative of this expression with respect to RL will set up the condition under what conditions the maximum power transfer takes place. The effort needed for such an approach can be quite tiresome and complicated. Fortunately, network shown in the figure above can be symbolized by an equivalent Thevenin’s voltage source as shown in figure below.
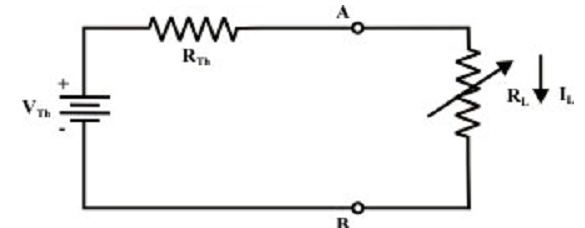
In figure above a variable load resistance RL is connected to an equivalent Thevenin circuit of original circuit. The current for any value of load resistance is,
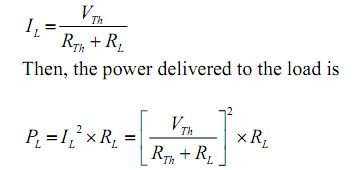
The load power based on both RTH and RL; though, RTH is constant for the equivalent Thevenin network. Therefore power delivered by the equivalent Thevenin network to the load resistor is completely based on the value of RL which absorbs a maximum power from the Thevenin circuit, we distinguish PL with respect to RL.

This outcome is termed as “Matching the load” or maximum power transfer takes place whenever the load resistance RL matches the Thevenin’s resistance RTH of a given systems. Also, notice that under the situation of maximum power transfer, load voltage is, by the voltage division, one-half of the Thevenin voltage. Expression for maximum power dissipated to the load resistance is provided by
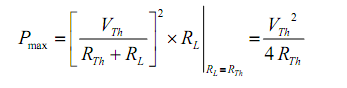
The total power conveyed by the source,
PT = IL2 (RTH + RL) = 2 x IL2RL
It means that the Thevenin voltage source itself dissipate as much power in its internal resistance RTH as the power absorbed by the load RL. The efficiency under maximum power transfer situation is given by,
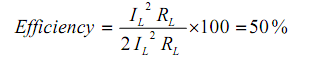
For a given circuit, VTH and RTH are fixed. By changing the load resistance RL, the power conveyed to the load differs as shown in figure below.
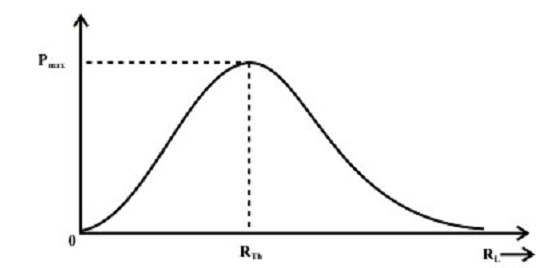
Figure: Power dissipated to the load as a function RL