Strain
The direct consequence of the application of load on a body will be the change in shape or size of the body. This change is named as deformation. For simplicity a bar of length L, like shown in given diagram (a) may be considered to undergo deformation beneath an axial load P. The length of the bar changes with an amount dL which can be called longitudinal deformation. The ratio of dL to L is defined as normal or direct strain.
That is:
ε = δL/L...........................................14
As shown in given diagram (a), dL is the increase in the length as the load P is a tension. If P were a compression load dL would have been reduce in the length. When dL is increment, e is tensile strain and when this is a decrement e is compressive strain. If the axis of the bar is along the x-axis, the stress caused by load will be sX, and accordingly the strain can be expressed like εx. Similarly, if the axis of the bar were along y- or z-axis, strain could be expressed as εy or εz.
Though, in such cases whereas there is only one stress component present as in case of given diagram (a) only one normal stress component is present, there will be only one strain component along with reference to longitudinal axis, and the suffixes of strain and stress may be omitted.
The effect of shearing stress is to reason a change in the shape or to distort the body as demonstrated in given diagram (b). The change in the original 900 angle among two sides is the measure of the strain that is termed as shearing strain in such case. From given diagram (b) the shearing strain, g, can be defined as,
γ = δ/L...........................................15
If the shearing stress causing strain is ΤXY, the shearing strain will be denoted like γxy .
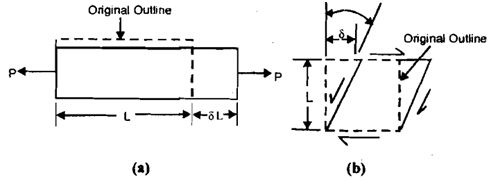
Diagram of Normal and Shearing Strain
The expressions for strains in eqn 14 and 15 are the measures of average values. If the strain at a point is to be explained, the expressions would change to.
ε = dδL/dL
γ = dδ/dL
From above diagram (a) this can be seen that while the tensile load P has caused a raise in length in axial direction, the transverse dimension has reduced. It shows that an axial strain would be accompanied by a transverse strain of opposite type that is if, the axial strain were compressive the transverse strain would be tensile. The magnitudes of transverse and axial strain bear a constant ratio that is termed as Poisson's ratio and is indicated by v.
v = magnitudes of transverse strain/ magnitudes of axial strain.......................16
Ratio of Poisson is an elastic constant of material and it varies from one material to other.
Like strain, stress at a point will also have 9 components in a common three-dimensional body. This is apparent from its definition as 'the ratio of change in length to original length'. Because the change in length and original length both have three components each along three coordinates of reference, their ratio will have nine components. Again because of symmetric nature, these nine components are reduced to six. These strain components are presented by ε if direct and g if shearing ε x, ε y and εy are direct strain components. γxy , γyzand γxz are shearing strain components. In plain strain state ε x = γxz = γyz = 0. This may be understood at such stage that even for the case of plane stress state as depicted in previous diagram (b) the strains will be three dimensional. The sX and sY stresses along x and y-axes, will cause also strain normal to x-y plane because of Poisson's ratio effect. Obviously the deformation in the z-direction that is normal to x-y plane may be restrained but only if a stress in the z-direction is applied. Hence a stat of plane strain in which strains only in x-y plane will be exists may be acquired with stress sz being present.
This is worthwhile to remind readers that the engineering materials which we employ to make machines are elastic whereas elasticity is understood as a property by virtue of which a deformed body regains its original size and shape while the deforming force is removed. The deformation that vanishes on removal of load is named as elastic deformation. This is, of course, implied that if stress is continuously raised, then at specific value of stress the plastic or non-recoverable deformation will begin. Minimum stress level or stage at which the plastic deformation sets in is termed as elastic limit. We have already seen that "in elastic limit stress is proportional to strain". This is the law of Hooke and is source of definition of elastic module. According to such law:
σ= Eε or E = σ/ε.............................................17
Τ = Gγ or G = Τ/γ............................................ 18
Whereas E is modules of elasticity or Young's modules and G are modules of rigidity or shear modules.
Therefore, E, G and g are three elastic constants. Along with a fourth constant, named as bulk modules or k, the number of elastic constants is four. The bulk modules are defined as like ratio of volumetric stress to volumetric strain. No confusion should arise for types of these strain and stress as the volumetric stress is nothing however pressure acting on the surface and volumetric strain is change in volume to original volume. Hence the volumetric stress is normal or direct stress. An isotropic material has only two independent elastic constant any two of four. If we suppose E and V are independent
After that:
G = E/{2(1 + v)}........................................19
K = E/{3(1 + 2v)}.......................................20
We should keep in mind that metallic materials we employ to make machine parts are essentially treated like isotropic and all are loaded in elastic limit. After that are some plastics, which may not be isotropic, although by reinforcing them along with randomly distributed fibers. Particles, fillers and plasticiser they are brought close to having isotropicity.