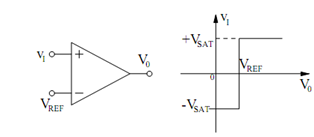
Non-inverting Comparator:

Figure (a) illustrates the circuit diagram of an op-amp utilized as a non-inverting comparator. The output voltage of the circuit is given by

                                                    v₀  = V_SAT sgn (V_I - V_REF )

The graph of v₀ versus v_I  is given in Figure

(a)                                            (b)

Figure: (a) Non-inverting Comparator; and (b) Plot of v₀ Versus v_I.

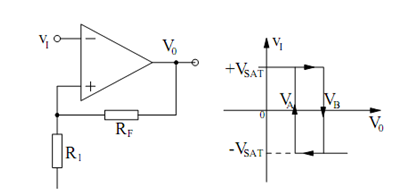
Positive feedback is frequently utilized with comparator circuits. The feedback is applied through the output to the non-inverting input of the op-amp. It is in contrast to the circuits covered in the preceding sections where feedback is applied to the inverting input. (The non-inverting integrator is an exception that uses feedback to both op-amp inputs.) Figure (a) gives the circuit diagram of an inverting op-amp comparator with positive feedback. The circuit is also called as a Schmidt trigger. The capacitor C_F in the figure is supposed to be an open circuit in the following. This capacitor is frequently used to develop the switching speed of a comparator by enhancing the amount of positive feedback at high frequencies. It has no effect on the input voltage at which the op-amp switches states.

(a)                                                  (b)

Figure: (a) Inverting Comparator with Positive Feedback; and (b) Plot of v0 Versus vI.

The output voltage from the circuit of Figure (a) may be written

                         v₀  = V_SAT sgn (V₊  - V_I )

Because v₀ has two stable states, v₀ = +VSAT and v₀ = - VSAT, it follows that v_I may have two stable states given by

V_A   = V _REF ( R_F / (R_F +R₁)  ) - V_SAT (R₁ /R_F  + R₁)

V_B   = V _REF ( R_F / (R_F +R₁)  ) - V_SAT (R₁ /R_F  + R₁)

where superposition and voltage division have been used for each equation. For

v_I  < V_A, it follows that v₀ = +V_SAT. For v_I > V_B, it follows that v₀ = - V_SAT. For V_A < v_I < V_B, v₀ may have two stable states, i.e. v₀ = ± V_SAT. The graph of v₀ versus v_I is given in Figure (b).

The value of v₀ for V_A < v_I   < V_B based on whether v_I   enhance from a value less than V_A or v_I reduce from a value greater than V_B. that is, the circuit has memory. If v_I  < V_A, primarily and v_I starts to increase, v₀ remains at the + V_SAT   state until v_I   becomes greater than V_B. At this point, v₀ switches to the - V_SAT   state. If v_I > V_B primarily and v_I starts to decrease, v₀  remains at the - V_SAT   state until v_I becomes less than V_A. Then v₀ switches to the + V_SAT state. The path for v₀ on the graph in Figure (b) is mentioned with arrows. The loop in the graph is commonly called a hysteresis loop.