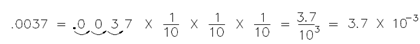Writing Numbers in Scientific Notation:

For transform numbers from decimal form to scientific notation, it must be remembered in which the laws of exponents form the primary for calculations using powers.

Using the output of the previous chapter, the subsequent whole numbers and decimals could be expressed as powers of 10:

1 =10⁰             0.1 = 1/10 = 10^-1

10 =10¹           0.01 = 1/100 = 10^-2

100 =10²         0.001 = 1/1000 = 10^-3

1000 =10³

10,000 =10⁴

A number N is within scientific notation while it is expressed as the product of a decimal number among 1 and 10 and some integer power of 10.

N = a x 10ⁿ    where 1 ≤ a < 10 and n is an integer.

An steps for converting to scientific notation are as follows:

Step 1: Place  an  decimal  instantly  to  the  right  of  the  left-most  non-zero number.

Step 2: Count the number of digits among the old and new decimal point.

Step 3: the exponent is positive if the decimal is shifted to the left,.  If the decimal is shifted to the right, the exponent is negative.

Now let us examine the logic of this.  Consider as an example the number 3750.  The number will not be changed if it is multiplied by 1000 and divided by 1000 (the net effect is to multiply it by one).  Then,

 3750/1000 × 1000      3.750 × 1000   3.750 × 10³

There is a division through 10 for each space the decimal point is moved to the left, that is compensated for through multiplying by 10.  Same, for a number such as .0037, we multiply the number by 10 for every space the decimal point is moved to the right.  Therefore, the number must be divided by 10 for each space.