Robot arms

Robot arms are called as manipulators technically. Some of the robots, especially industrial robots, are nothing more than the sophisticated manipulators. A robot arm is categorized according to its geometry. Some of the manipulators resemble human arms. The joints in these machines are given names like shoulder, elbow, and wrist. Other manipulators are much different from the human arms that these names do not make sense. An arm which employs revolute geometry is similar to the human arm, with a shoulder, elbow, and wrist. An arm having cartesian geometry is very different from the human arm, and moves along axes (x, y, z) which can be best described as up- and-down, right-and-left, and front-to-back.

Degrees of freedom
The term degrees of freedom refer to number of different ways in which a robot manipulator can move. Most manipulators move in three dimensions, but they have more than three degrees of freedom. You can use your own arm to obtain an idea of the degrees of freedom which a robot arm might have. Extend your right arm straight out toward horizon. Extend your index finger such that it is pointing. Keep your arm straight, and move it from shoulder. You can move in 3 ways. Up-and-down movement is called as pitch. Movement to right and left is called as yaw. You can rotate your whole arm as if you were using it as screwdriver. This motion is called as roll. Your shoulder thus has 3 degrees of freedom which are- pitch, yaw, and roll.

Now move your arm from elbow only. This is difficult to do without moving your shoulder along. Holding your shoulder in same position constantly, you will see that the elbow joint has the equivalent of pitch in the shoulder joint. But that is all. Your elbow, thus, has one degree of freedom.Extend your arm toward horizon again. Now move your wrist only. Try to keep the arm above wrist straight and motionless.  Your wrist can bend up and down, side to side, and it can twist a little. Your lower arm has same 3 degrees of freedom which your shoulder has, although its roll capability is restricted.

In total, your arm has 7 degrees of freedom: 3 in the shoulder, one in the elbow, and 3 in the arm below the elbow.You may think that a robot should never require more than 3 degrees of freedom. But extra possible motions, given by multiple joints, give a robot arm versatility that it could not have with only 3 degrees of freedom.

Degrees  of rotation
The degrees of rotation refers to the extent to which the robot joint, or a set of robot joints, can turn clockwise or counterclockwise about the prescribed axis. Some reference point is used, and the angles are given in the degrees with respect to the joint.Rotation in 1 direction (clockwise) is represented by the positive angles;
rotation in opposite direction can be specified by negative angles. Therefore, if angle X 58 °, it refers to a rotation of 58 °clockwise with respect to the reference axis. If angle Y     274 °, it refers to a rotation of 74 °counter clockwise.Figure given below shows a robot arm with 3 joints. The reference axes are J1, J2, and J3, for the rotation angles X, Y, and Z. The individual angles get added together. To move this robot arm to certain position within the work envelope, or region in space which the arm can reach, the operator enters data into the computer. This data includes the measures of angles X, Y, and Z. The operator has specified X   =  39, Y =    75, and Z   =  51. In this instance, no other parameters are shown. But there would be variables such as the length of arm sections, base rotation angle, and position of the robot gripper.

Articulated geometry
The word articulated means broken into the sections by joints. A robot arm with the articulated geometry bears some resemblance to arm of a human. The versatility can be defined in the terms of number of degrees of freedom. For instance, an arm might

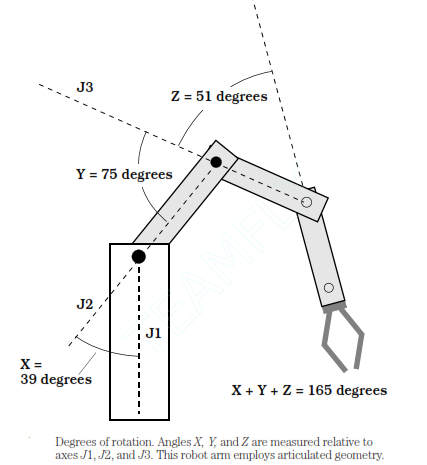
have 3 degrees of freedom: base rotation (equivalent of azimuth), elevation angle, and reach (equivalent of radius). If you are a mathematician, you may recognize this as a spherical coordinate scheme. There are much different articulated geometry for the given number of degrees of freedom. The given figure is a simplified drawing of a robot arm which uses articulated geometry.