Series RLC Circuit:

The applied voltage is v = V_m  sin ωt

Inductive reactance  X _L  = ωL

 Capacitive reactance X _C  =1 / ωC

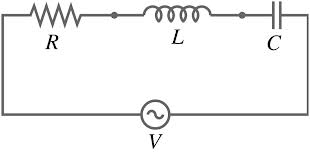
Figure: Series RLC Circuit

Here, we describe the impedance of the circuit which is given by

Z = R + j ( X _L  - X _C )   in ohm

The magnitude of the impedance is

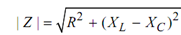
and angle

θ= tan ^-1 (X _L  - X _C) / R

This is the angle between the applied voltage v and the current i. θ is also termed as the power factor angle of the circuit.

The current i is specified by

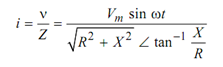
where X = X_L - X_C

 or        i = (V_m /| Z | ) sin  (ωt - tan ^-1 ( X /R)

If the circuit in inductive (X_L > X_C) then current i lags the v by angle tan ^-1 (X/ R)  . But if the circuit is capacitive then i leads the v by angle tan ^-1 (X/ R)  .

The voltage drop across each passive elements

V_R = i R,           V_L = X_L i,           V_C = X_C i

Also       v¯ = v¯ _R  + v¯ _L  + v¯ _C    (Kirchhoff's Voltage Law)

Generally, if we apply Kirchhoff's voltage law in series RLC circuit then KVL equation is given by

v = R i + L di/ dt +  (1 / C )∫ i dt