Objectives of Loading Problems

In any type of manufacturing system, there are different objectives associated along with machine loading problems, as:

(a) Minimization of work in process or WIP inventory

(b) Maximization of load balance

(c) Maximization of system throughput

(d) Minimization of Make span

(e) Minimization of system unbalance

(f) Maximization of profit

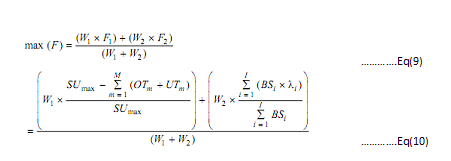
In the present chapter, two subjective namely minimization of system unbalance and maximization of throughput are taken, where system disturb or unbalance is the net sum of remaining time on all machines after allocation of each operation of the task and throughput is the total of the batch size of the chosen jobs. Minimum value of system disturbs or unbalance can be zero this is worth to mention that overloading of the machines is permitted and the maximum value of the throughput is while each job get chosen. Mathematically, the afore-mentioned objective can be written like:

System unbalance or US

In the afore-mentioned equation, UT_m denotes the underutilized time upon machine m and OT_m is the over-utilized time on machine m. The index of machine is m.

Throughput or TH

BS_i is the batch size of job i and λ is the decision variable equivalents 1, if job is chosen for processing, or else 0. Because, in the afore-mentioned objectives, system disturb or unbalance is to be minimum and throughput is to be maximum, hence, an overall weighted objective function is formed via transforming the minimization of system disturb or unbalance value into the maximization of system balance value, described as:

Here, SU_max is the maximum possible value of system unbalance

hence, the overall objective function will be,

A step-wise process to calculate the afore-mentioned objectives is described as:

Step 1

Input the total number of machines m_max, here m is the index for machines,

m = 1, 2, . . . , m_max. For m = 1 to m_max, input the ATM_M and ATS_M, where, ATM_M   = Available machining time on machine m, ATS_M = available tools slots on machine m.

Step 2

Input the job sequence having j_max jobs arranged at k_max positions, here j is the index for task, j = 1 to j_max, and k is the index for the location of the part type in the manner, k = 1 to k_max.

Step 3

Initialize K = 1, and O = 1.

Step 4

As per to the input sequence, for the job j at k^th position, If the task contains necessary operation,

Then for the necessary operation O, find out ETM_jom, ETS_jom, ATM_m, ATS_m, here, ETM_jom is the important time requirement of job j for operation O on machine m, ETM_jom is the important tool slot requirement of job j for operation O upon machine m.

Step 5

If ATS_m ≥ ETS_jom,

Then go to Step 6,

Else, reject the job j (tool slot constraints) and increase index k by 1 (i.e. k = k + 1)

and goto Step 4.

Step 6

If ATM_m ≥ ETM_jom,

Then assign the necessary operation o of the job on machine m. find out RTM_m, RTS_m, where, RTM_m is the keep time on the machine m and RTS_m is the saying tool slot on machine m after the allocation. At this time, update the available time and tool slot, consequent to machine m, that is (ATM_m = RTM_m and ATS_m = RTS_m).

Else determine SUjom, where, SUjom is the system unbalance after allocation of O^th

operation of job j on machine m.

If (SU_jom < 0),

Then refuse the job j (negative system unbalance), now increase k by 1 (k = k + 1), Go to Step 4.

Else allocate the necessary operation O of job J upon machine m. find out RTMm, and RTSm and update the obtainable time and tool slot to the corresponding that is

ATM_m = RTM_m and ATM_m = RTM_m.

Step 7

If O < O_max

Then increase O by 1 (that is O = O + 1) and go to Step 6.

Else go to Step 8.

Step 8

Find out OTM_JOM and OTS_JOM for the entire optional operations o (that is set of operations that have more than one machine as an option to process). O = 1 to O_max, OTM_JOM is the machining time of the optional operation O of the job j on machine m. and OTS_JOM is the machining time of the optional operation O of the job j upon machine m.

Step 9

Initialize O = 1;

Step 10

If (ATM_m ≥ OTM_jom), Then go to Step 11, Else evaluate SU,

If (SU > 0)

Then go to Step 11,

Else reject the job (negative system unbalance), and set k = k + 1, and go to Step 4.

Step 11

If (ATS_m ≥ OTS_jom)

Then assign the optional operation O of job j on machine m. find out RTM_m, RTS_m after allocation. Set (ATM_m = RTM_m, and ATS_m = RTS_m) go to

Step 12.

Else reject the job j (tool slot constraint), set k = k + 1.

Step 12

If (O < O_max),

Then set O = O + 1, go to Step 10,

Else go to Step 13.

Step 13

If (k < k_max)

Then go to Step 2,

Else go to Step 14.

Step 14

Find out system unbalance SU, Throughput TH, set of assigned jobs and set of jobs rejected due to tool slot constraint (JR_TSC) and negative system unbalance (JR_NSU).

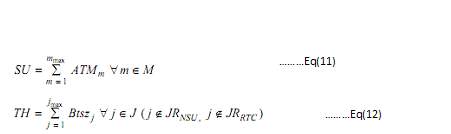
Step 15

As per to objective function, evaluate the fitness value.

                                                                       Table no.1: Initial Available Data