Problems that can be resolved by using ACO

A huge range of problems can be resolved by using this kind of approach. All of these problems related to the group of shortest path problems such can be characterized by the given aspects as:

(a) There is a set of constraints W explained for the problem being resolved.

(b) There is a finite set of components N = {n₁, n₂, . . . , n_i}.

(c) The problem presents various states explained upon ordered components sequences ∂ = < n_r, n_s, . . . , n_u, . . . > (< r, s, . . . , u . . . > to make simpler) over the elements of N. We denote by Δ the set of feasible states, if Δ is the set of all probable sequences. | ∂ | is the length of a sequence ∂ that is in the sequence, the number of components.

(d)There is a neighborhood structure defined as given as: ∂₂ is a neighbor of ∂₁ in one logical movement that implies that, if r is the last component of the order ∂₁, there should exist a component s ∈ Y such as ∂₂ ≤ ∂₁, s >  that is there exists a valid transition among r and s. The feasible neighborhood of ∂1 is the set containing each sequence ∂₂ ∈ Δ; if ∂₂ ∉Δ , we can say as ∂₂ is in the infeasible neighborhood of ∂₁.

(e) A solution S is an element of Δ verifies all the problem needs.

(f) There is a cost C (s) associated along with each solution S.

(g)In several cases, a cost or an estimate of the cost may be corresponding to states. Combinatorial optimization problems can be presented in the form of a weighted graph G = (N, A), here A is the set of edges such connects the set of components N, can be solved by using Ant Colony Optimization. The graph G is named as also construction graph G. Thus,

(a)The components n_r is the nodes of the graph.

(b)The states ∂ and solutions S associates to paths in the graph, i.e. sequences of nodes or edges.

(c)The edges of the graph a_rs, are transitions/connections defining the neighborhood structure. ∂₂ ≤ ∂₁, s > is a neighbor of ∂1 and edge a_rs, exists in the graph.

(d)There might be explicit transition costs C_rs, corresponding to each edge.

(e)The components and connections might have corresponding pheromone trails τ, which represent several form of indirect, long term memory of the search process, and heuristic values η that represent several heuristics information obtainable on the problem beneath solution.

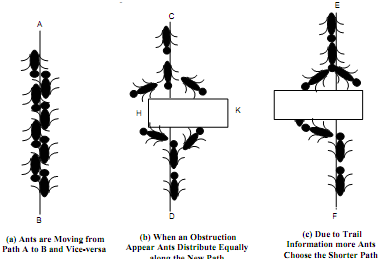
                            Figure: Mechanism Adopted by Colony of Ants in Search of Food