Parallel Opposing:

Figure illustrates two coils coupled in parallel where the mutually induced e.m.f in a coil because of change in current in the other coil is negative.

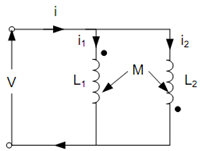
Figure: Inductive Coupling in Parallel (Flux Opposing)

Using Kirchoff's voltage law, we can write

V = L₁ (di₁/dt)  - M (di₂/ dt)

Also,

V = L₂ (di₂/dt)  - M (di₁/ dt)

From Eqs. (53) and (54), we get

L ( di₁ /dt) - M di₂  /dt = L₂ (di₂/dt)  - M (di₁/ dt) ---- (60)

Now

i = i₁  + i₂

i₂  = i - i₁

Substituting i₂ from Eq. (56) in Eq. (55), we obtain

L  di₁/dt  - M d (i - i₁ )/dt = L₂ + d (i - i₁ ) - M(di₁/dt)

L  di₁/dt  - M d i /dt  + M d i /dt  = L₂ + di /dt  - M(di₁/dt)

(L₁  + L₂  + 2M )  di₁/dt  = (L2  + M )  di₁/dt

∴          di₁ /dt  = ( (L₂  + M )/(L₁ + L₂  + 2M)  (di /dt  )

Likewise,         di₂ /dt      = (L₁+M/ L₁ + L₂ + 2M  ) di/dt

Using Eqs. (57) and (58) in Eq. (53), we obtain

 V = L₁ (L₂  + M/ L₁ + L₂  +2M) di/dt + M(L₁ + M )  /  (L₁ + L₂  + 2M ) (di/dt)

or, V =   (L₁ L₂  + L ₁M + L₁ M - M ²)   / (L₁ + L₂  +2M)            di/dt

or V =   (L₁ L₂  - M² )/ (L₁ + L₂  + 2M)  di/dt

Let L be the equivalent inductance of the parallel combination, then we can write

V = L (di /dt)

From Eqs. (61) and (62), we obtain

 L (di/dt ) =   (L₁ L₂  - M² )/ (L₁ + L₂  + 2M) di/dt                    

L =   (L₁ L₂ - M²)/ (L₁ + L₂ +2M)