Parallel Aiding:

Figure illustrates two coils coupled in parallel where the fluxes are additive as per dot convention.

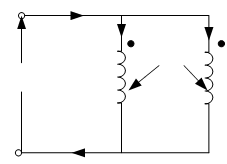
Figure: Inductive Coupling in Parallel (Flux Aiding)

Using Kirchoff's voltage law, we may write

V = L₁ (di₁/ dt ) + M (di₂/ dt)

Also,

V = L ₂(di₂/ dt ) + M (di₁/ dt)

From Eqs. (2.42) and (2.43), we get

L  (di₁/ dt ) + M( di₂/ dt)  = L (di₂/ dt ) + M( di₁/ dt )

Now

∴ i = i₁  + i₂

i₂  = i - i₁

Substituting i₂ from Eq. (45) in Eq. (44), we obtain

L₁  (di₁/ dt)  + M d (i - i₁ )/ dt = L₂ d (i - i₁ ) / dt + M (di₁/ dt)

Or, L₁  (di₁/ dt)  + M di / dt  - M di₁ / dt = L₂ (di / dt) - L₂ (di₁ / dt )+ M (di₁/ dt)

or,  (L ₁ + L₂  - 2M )  (di₁ /dt) = (L₂  - M )  di₁/dt

∴          di₂/dt  = ((L₂  - M )/ (L₁ + L₂  - 2M )) di₁/ dt

Similarly,

di₂ /dt =  ((L₁ - M )/ L₁ + L₂  - 2M)  di/dt

Using Eqs. (46) and (47) in Eq. (42), we get

V = L₁ (L₂  - M/ L₁ + L₂  - 2M) di/dt + M(L₁ - M )  /  (L₁ + L₂  - 2M ) (di/dt)

or, V =   (L₁ L₂  - L ₁M + L₁ M - M ₂)   / (L₁ + L₂  - 2M)           di/dt

or V =   (L₁ L₂  - M² )/ (L₁ + L₂  - 2M)  di/dt

Let L be the equivalent inductance of the parallel combination, then we may write

V = L (di /dt)

From Eqs. (50) and (51), we obtain

L (di/dt ) =   (L₁ L₂  - M² )/ (L₁ + L₂  - 2M) di/dt                    

L =   (L₁ L₂ - M²)/ (L₁ + L₂ - 2M)