Two Isolated Coils:

Let current i₁ is alternating current and producing flux φ₁  (per turn).

Then           φ₁  = φ₁₁ + φ₁₂

where φ ₁₁ = flux linked with coil 1 only (leakage flux), and

φ ₁₂ = flux reaches to coil 2 (mutual or useful flux).

Now the emf is induced in both the coils. In coil 1, emf e₁ is induced because of its self inductance L₁ and in coil 2 emf e₂ is induced because of mutual inductance M between coils 1 and 2.

e₁  = L₁ di₁ / dt                      (by Eq. (4))

Likewise, we may write the expression for e₂

 e₂ = M (di₁ /dt)

where M = mutual inductance among coils 1 and 2 (in henry)

e₂ may also be written as :

e₂   = N ₂ d φ₁₂ / dt

On equating Eqs. (6) and (7)

M  di₁/ dt = N₂ (d φ₁₂ /dt)

⇒         M = N₂ (d φ₁₂ /di₁)

 Assuming the zero initial conditions

M = N₂ (φ₁₂/ i₂)

Now consider the reverse case, in which we give the supply to the secondary coil and finding the induced emf in primary coil.

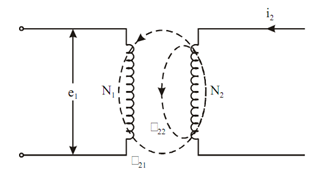
Figure: Two Isolated Coils with Current i₂

φ₂  = φ₂₁ + φ₂₂     

Where φ ₂₁ = mutual flux,

φ ₂₂  = leakage flux, and

φ ₂ = total flux produced by i₂.

So the induced emf

e₂ = L₂  ( di₂ /dt)

 (because of self inductance L2 of the coil).