Inductances in Series and Parallel:

Inductances in Series

 (a) Let the two coils be linked in series such that their fluxes are additive,

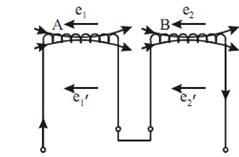
Figure: Series Inductors          

Self induced emf in A = e₁ = - L₁(di /dt)

Mutually induced emf in A due to change in B = e₁′ = - M (di/ dt)

Self induced emf in     B₂ = e₂ = - L₂   (di/ dt)

Mutually induced emf in B because of change in A₂ = e₂′ = - M  (di/ dt)

Total induced emf  =- di /dt  (L₁ + L₂ + 2M )

If L refers to the equivalent inductance then total induced emf in that single coil is given as,

                           =- L di /dt

From Eqs. (22) and (23) we get

L = (L₁ + L₂  + 2M )

 (b)       While coils are so connected that their fluxes are in opposite direction,

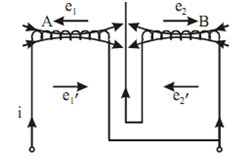
Figure: Inductor in Series Opposition

Now,

e₁=-L₁ (di/dt) and e₁' = M (di/dt)

e₂ = L₂ (di/dt) and e₂' = M (di/dt)

Total induced emf  =-(di/dt)  (L₁ + L₂ - 2M )

∴ Equivalent inductance L = L₁ + L₂  - 2M