Complex Numbers:
Complex numbers are numbers which consist of a real part and an imaginary part. The solution of a few quadratic and higher degree equations results in complex numbers. For instance, the roots of the quadratic equation, x2 - 4x + 13 = 0, are complex numbers. Using the quadratic formula yields two complex numbers as roots.
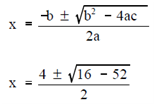
X = (4±√-36)/2
X = 4±6i/2
X = 2±3i
The two roots are 2 + 3i and 2 - 3i; that are both complex numbers. 2 is the real part; +3i & -3i are the imaginary parts. The common form of a complex number is a + bi, in that "a" represents the real part and "bi" represents the imaginary part.
Complex numbers are added, subtracted, multiplied & divided like algebraic binomials. Therefore, the sum of the two complex numbers, 7 + 5i and 2 + 3i is 9 + 8i, and 7 + 5i minus 2 + 3i, is 5 + 2i. Similarly, the product of 7 + 5i and 2 + 3i is 14 + 31i +15i2. But i2 equals -1. Therefore, the product is 14 + 31i + 15(-1) which equals -1 + 31i.