Evaluation of Fuzzy IF-THEN Rules

Look at the problem of evaluating a fuzzy IF-THEN rule as:

μ_{A ⇒ B}  (a, b) namely μ_A  (a) ⇒ μ_B  (b), a ∈ A, b ∈ B

For classical two valued logic, this evaluation is easy as:

μ_B(b) = 1 if μ_A  (a) = 1,

And     0  if μ_A(a) = 0.

That is,

"a ∈ A ⇒ b ∈ B," and

μ_B¯ (b) = 1 if μ_A  (a) = 1,

And       0 if μ_A (a) = 0.

As is, "a ∉ A ⇒ b ∈ B ."

Though, for fuzzy logic, according to the alternative of particular logical system, there are some options for the IF-THEN rule

" μ_A(a) ⇒ μ_A(a) "

 As like:

• μ_{A ⇒ B} (a, b) = min {μ_A (a), μ_B (b)} ;
• μ_{A ⇒ B} (a, b) = μ_A (a), μ_B(b) ;
• μ_{A ⇒ B} (a, b) = min {1, 1 + μ_B(b) - μ _A (a)} ;
• μ_{A ⇒ B} (a, b) = max {min {μ _A(a), μ_B (b)}, 1 - μ _A(a)} ;
• μ_{A ⇒ B} (a, b) = max {1 - μ _A(a), μ_B (b)} ;
• Goguen's formula is:

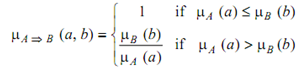
Each these evaluation formulas are valid for the fuzzy logic inference purpose, provided one employs consistently the similar formula for the implication relation ⇒. Obviously, different formulas give various resulting values, which merely imply various degrees of inference based on various logical systems, however not the validity of the answers. Of course, formulas (a) and (b) are extremely simple to employ; but they are the similar as the logical AND operation ∧, formulas (d) and (f) appear too complicated. The most general one is formula (c).