Application Of Tabu-Search In Outsourcing Problem

In order to demonstrate the application of Tabu search in combinatorial optimization problem, a manufacturing unit having of five machines {M₁, M₂, M₃, M₄, M₅}, has been taken. Machine M₅ is an outsourcing machine and one-way transportation time between outsourcing and manufacturing machine is 5 units. If due dates of customer's order that is made of eight various jobs produced by 20 various operations are D1 ≤ 55 and their delivery and assembly time are AT₁ = DD₁ = 10, after that in order to produce customer order as per to their due date, make span of the operation sequence should be less than 35. Alternative machines subsequent to each operation and their machining time are displayed in Table no.2, while, precedence relationship among different operations are displayed in Figure no.4. In outsourcing problem, the detailed steps of applying the Tabu-search are described below:

                            Table no.2: Details of Jobs, Operations, Processing Time for Prismatic Part

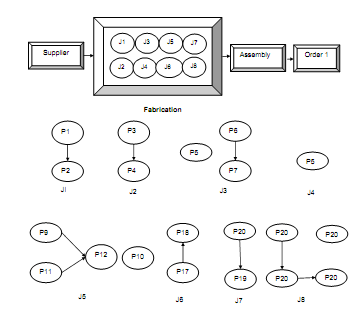
                            Figure: Directed Graph of a Manufacturing Process with Precedence

Steps for Implementing Tabu Search to an Outsourcing Problem

Step 1:   Generate an initial feasible solution and allocate it to Sol.

Determine its make span value MT (Sol).

Step 2:    Initialize T = T₀ = 300; K = 1; TL = ?; Reject = 0;

Sol_b = Sol.

Step 3:    Generate

Sol_P, Sol) that is Generates new solution from the existing one.

Step 4:     If pre-treated solution is feasible one that is Sol_P satisfies all the conditions then go to next step else go to Step 3 and make a new solution.

Step 5:   If Sol_p ∈ TL

Then go to Step 6

Else go to Step 7.

Step 6:     If MT (Sol_P) ≥ A

Then, go to Step 7

Else, go to Step 3.

Step 7:     ?MT = MT (Sol_P) - MT (Sol)

If ?MT ≥ 0, Then, go to Step 8.

Step 8:    allocate

Sol = Sol_P.

involve Sol_p in tabu-list

TL ← Sol_p

Update aspiration

A ← MT (Sol_P).

Step 9  :    ?MT_b = MT (Sol_P) - MT (Sol_b) If, ?MT_b ≥ 0

Then go to Step 10

Else, go to Step 14.

Step 10   :  allocate

Sol_b = Sol_p

Reject ← 0

go to Step 14.

Step 11  :   calculate

Transition Probability or TP

Generate a random number R in between (0, 1) If (TP ≤ R)

go to Step 13

else go to next step.

Step 12   :  Assign

Sol = Sol_P

Include SolP in tabu list

A ← MT (Sol_P).

Step 13   :  Reject = Reject + 1; If Reject ≥ 3

go to Step 15

else go to  Step14.

Step 14   :  K = K + 1;

Change the temperature

T = T₀⁄(1 + ln_K) If K ≥ 20

go to Step 15

else go to Step 3.

Step 15   : FREEZE

Sol_b is the near optimal solution.