Voltages across series resistances
The bulbs in the string of Figure given below, being all same, each get the same amount of voltage from source. If there are a dozen of bulbs in a 120-V circuit, each bulb will possess a potential difference of 10 V across it. This will be true no matter how large or small the bulbs are, as long as they are all identical.
If you think about this for a moment, it is easy to see why it is true. Look at the schematic diagram of Figure. Each resistor carries the same current, each resistor Rn has a potential difference En across it, equal to the product of current and resistance of that particular resistor. This En's are in series, like cells in the battery, so that they get added together. What if En's across all resistors added up to something more or less than the actual supply voltage, E? Then there would have to be a "phantom EMF" some place, may be adding or taking away voltage. But there is no such.
Look at another way. The voltmeter V in Figure shows the voltage E of the battery, because the meter is hooked up across the battery. The meter V also shows the sum of the En's across set of resistors, as it is connected across the set of resistors. The meter says the same thing whether you think of it as measuring the battery voltage E, or as measuring the sum of the En's across series combination of resistors. Thus, E is equal to sum of the En's.
This is a fundamental rule in the series direct current circuits. It holds for 60-Hz utility alternating current circuits almost every time.
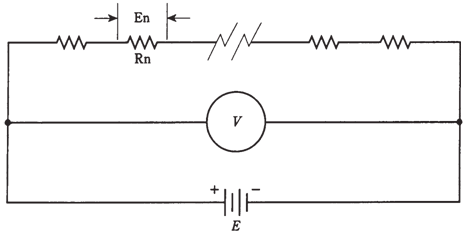
Figure-- Analysis of voltage in the series circuit
How do you find the voltage across any particular resistor Rn in a circuit like the one in the given Figure? Remember Ohm's Law for finding voltage: E = IR. The voltage is equal to product of current and resistance. Remember, that you should make use of volts, ohms, and amperes while making calculations. In order to find current in circuit, I, you are required to know the total resistance and supply voltage. Then I = E/R. First find current in whole circuit after that find voltage across any particular resistor.
Problem: 1
In the Figure given above, there are 10 resistors. Five of them have values of 10 Ω, and the other five have values of 20 Ω. The power source is direct current of15 V. What is the voltage across the 10 Ω resistors? Across one of the 20 Ω resistors?
1st, find total resistance: R = (10 * 5) + (20 * 5) = 50 + 100 = 150Ω. Then find current: I= E/R = 15/150 = 0.10 A = 100 mA. This is the current through each resistors in the circuit.
If Rn = 10 Ω, then En = I(Rn) = 0.1 * 10 = 1.0 V.
If Rn = 20 Ω, then En = I(Rn) = 0.1 * 20 = 2.0 V.
You can check that whether all of these voltages add up to supply voltage. There are 5 resistors with 1.0 V across each, for a total of 5.0 V; there are also 5 resistors with 2.0 V across each, for a total of 10 V. So the sum of the voltages across resistors is 5.0 V+ 10 V = 15 V.