Resistances in series-parallel
Sets of resistors, all are having identical ohmic values, can be connected together in parallel sets of series networks, or in series sets of parallel networks. By doing this, the total power handling capacity of resistance is greatly increased over that of a single resistor.
Sometimes, the total resistance of a series parallel network is same as value of any one of the resistors. This is always true if the components are identical, and are in a network termed as an n by n matrix. That means, when n is a whole number, there are total n parallel sets of n resistors in series, or we can also say that there are n series sets of n resistors in parallel. Either arrangement will give the same results in practice.
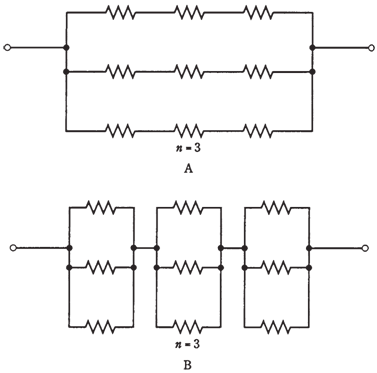
Figure-- Series parallel combinations. At A, sets of series resistors are connected in parallel. At B, sets of parallel resistors are in series.
Engineers and technicians sometimes use this to their advantage to get the resistors with the large power-handling capacity. Each resistor should have the same rating, assume it to be1 W. Then combination of n by n resistors will have n2 times that of a single resistor. A 3 * 3 series-parallel matrix of 2-W resistors can handle 32*2 = 9 * 2 = 18 W, for instance. A 10*10 array of 1-W resistors can take 100 W. The other way to look at this is to see that the total power-handling capacity is multiplied by total number of individual resistors in matrix. But this is true if all the resistors have the same ohmic values, and posses same power-dissipation ratings.
It is not wise to build series-parallel arrays from resistors having different ohmic values or power ratings. If resistors have values and ratings which are even a little nonuniform, one of them can be subjected to more current than it can withstand, and it will burn out. Then current distribution in network can change so a 2nd
component fails, and then a 3rd. It is difficult to predict that the current and power distribution in an array when its resistor values are all different. So it is tough to know whether any of components in such a matrix are going to burn out.
If you require a resistance having a certain power-handling capacity, you should be sure the network can handle at least that amount of power. If a 50-W rating is required, and some combination will handle 75 W, that's alright. But it is not good enough to build a circuit which will handle just 48 W. Some extra tolerance, say 10 percent over the minimum rating is needed, is good, but it is silly to make a 500-W network using far more resistors than required, unless that is the only convenient combination given to the parts which are available.
Nonsymmetrical series-parallel networks, which are made up from identical resistors, will increase the power handling capability of it. But in these cases, the whole resistance will not be the same as the value of the single resistors. The overall power-handling capacity will be always multiplied by total number of resistors, whether the network is symmetrical or non symmetrical, provided that all resistors are the same. In engineering, cases sometimes arise where nonsymmetrical networks fit the requirement just right.