Reducing complicated RLC circuits:
Sometimes you will see circuits in which there are several capacitors, resistors, and coils in series and parallel combinations. It is not intent here to analyze all the types of bizarre circuit situations. This will fill up hundreds of pages with diagrams, formulas, and calculations, and no one would ever read it.
A general rule is applied to complicated RLC circuits: Such a circuit can be reduced usually to an equivalent circuit which contains one resistor, one capacitor, and one inductor.
Series combinations:
Resistances in series simply add. Inductances in series add. Capacitances in series combine in a more complicated way. If you do not remember the formula, it is
1/C =1/C1 = 1/C2 ...= 1/Cn
where C1, C2, ..., Cn are individual capacitances and C is total capacitance. Once you have found 1/C, take its reciprocal to obtain the value of C.
An example of a complicated series RLC circuit is shown in the Figure given below. The equivalent circuit, with 1 resistor, 1 capacitor, and 1 coil, is shown in Figure given below.
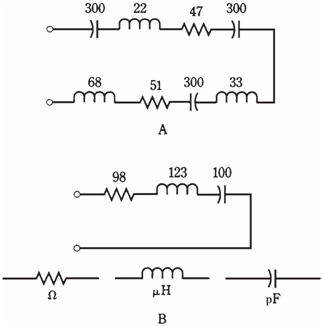
Figure-- At point A, a complicated series RLC circuit; at point B, the same circuit simplified.
Parallel combinations
In parallel, resistances and inductances combine in the manner capacitances do in series. Capacitances simply add up.
An example of a complicated parallel RLC circuit is shown in the Figure given below. The equivalent circuit, with one resistor, one coil and one capacitor, is shown in the Figure given below
Complicated, messy nightmares
Some RLC circuits do not fall neatly into either of above categories. An instance of such a circuit is shown in the Figure given below. How would you find complex impedance at some frequency, like 8.54 MHz?
You should not waste much time worrying about the circuits like this. But the given a frequency, a complex impedance does exist.
An engineer would use a computer to solve the particular problem. If a program did not already exist, the engineer would write one, or else hire it done by a professional programmer.
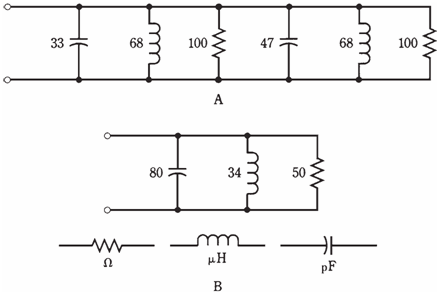
Figure-- A series-parallel RLC nightmare.
The other way to find complex impedance here would be to actually build the circuit, connect the signal generator to it, and measure R and X with an impedance bridge directly. Because the proof of pudding is in the eating, a performance test should eventually be done anyway, no matter how complicated the design theory. Engineers have to build things which work!