Power distribution in parallel circuits
When resistances are wired in parallel, they each consume power according to the same formula, P = I2R. But the current is not the same in each resistance. An easier method to find the power Pn, dissipated by resistor Rn, is by using the formula Pn = E2/Rn here E is the voltage of supply. Recall that this voltage is same across every resistor in a parallel circuit.
Problem:
Find the total power consumed of the resistor circuit in the above problem using two different methods.
The 1st method involves adding P1, P2, and P3. Let us use 4-significant-digit values for "error reduction insurance." The sum is P=0.4091+0.1915+0.13240=7330 W. This can be rounded to 0.73 W or 730 mW.
The 2nd method involves finding resistance R of parallel combination. You can do this calculation yourself, keeping track for four digits for insurance reasons, getting R = 12.28 Ω. Then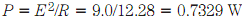 
. This can be rounded to 0.73W or 730 mW.
In mathematics and logic, the results are deduced from a few simple, intuitively appealing principles called as axioms. You maybe already know some of these, such as Euclid's geometry postulates. In electricity and electronics, complex circuit analysis can be made simple if you are acquainted with some axioms, or laws. You have seen some of these already. They are as follows:
- The current in the series circuit is same at every point along the way.
- The voltage across any component in the parallel circuit is same as the voltage across some other, or across the whole set.
- The voltages across elements in a series circuit add up to the supply voltage.
- The currents through elements in the parallel circuit always add up to the total current drawn from the supply.
- The total power consumed in the series or parallel circuit is always equal to the sum of the wattages dissipated in each of the elements.
The two famous laws in electricity and electronics are illustrated below. These make it possible to analyze very complicated network of series parallel. That is not what you will be doing in this course, but given the previous axioms and Kirchhoff's Laws which follow, you could if you had to.