Power and the watt

When the current flows through a resistance, heat results. This is inevitable. The heat energy can be measured in the unit watts, denoted by W, and represents electrical power. Power can be manifested in many other ways, like in the form of mechanical motion, or radio waves, or visible light, or noise. In fact, there are dozens of different ways that power can be dissipated. But heat is present, in addition to other form of power in the electrical or electronic device. This is because no equipment is 100 % efficient. Some power always goes to waste, and this waste is in form of heat.

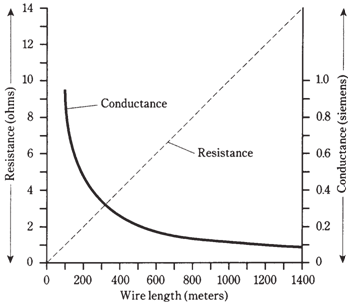
Graph--   Total resistances and conductances for a wire having 10 ohms of resistivity per kilometer.

Look at the diagram given above. There is a some voltage across the resistor, not given in the diagram specifically. There is a current flowing through resistance, not quantified in diagram. Assume that we call the voltage E and the current I, in volts and amperes, respectively. Then the power in watts dissipated by resistance, call it P, is the product E*I. This means that: P=EI.

This power may all be heat. Or it may be in various forms, like heat, light and infrared. This would be the state of affairs if resistor were an incandescent light bulb, for instance. If it were a motor, some power would exist in the form of mechanical work.

If voltage across resistance is caused by 2 flashlight cells in series, giving 3 V, and if current through the resistance is 0.1 A, then E=3 and I=0.1, and we can compute the power P, in watts, as:

(watts) = EI = 3*0.1 = 0.3 W

Assume that the voltage is 117 V, and current is 855 mA. To compute the power, we should convert the current into amperes; 855 mA=855/1000 = 0.855 A. Then

P (watts) = 117*0.855 = 100 W

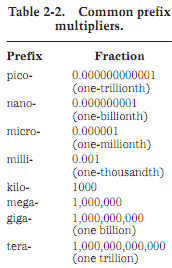
You will hear about milliwatts  (mW), microwatts (µW), kilowatts (kW) and megawatts (MW). One should, be capable tell from prefixes what these units are signifinf. But in case you have not gotten the idea yet, you can refer to the given table. This table gives the commonly used prefix multipliers in electricity and electronics, and fractions which they represent. Hence, 1 mW = 0.001 W; 1 kW = 1,000 W; and 1 MW = 1,000 kW =1,000, 000 W. 

At times you need to use the power equation to find the voltages or currents. Then you should use I=P/E to find current or E=P/I to find power. It is easiest to remember that P    EI, and derive the other equations from this by dividing through either by E or by I.

Browse important topics or keywords of Power below: