Design of Slideways

Slideways are designed for wear resistance and stiffness.

Design of Slideways for Wear Resistance

The wear resistance of slideways is principally dependent upon maximum pressure acting upon the mating surfaces. This condition may be described as

Equation 1

 p_max ≤ P_mp

In which

p_m stands for maximum pressure acting on the mating surface, and

p_mp stands for permissible value of the maximum pressure.

It is seen during the consequent analysis that slide-way designed for maximum pressure is quite complicated. Occasionally, this design is replaced by a simple procedure based on the average pressure acting upon the mating surfaces. The condition is that:

 Equation 2

P_a ≤ P_ap

In which

p_a stands for average pressure acting on the mating surface, and  

p_ap stands for permissible value of the average pressure.

Therefore from Equation (1) and (2), the design of slideways for wear resistance requires that

(1) p_m and pa to be known,

(2) p_mp and pap to be known, and

(3) The values of p_mp and pap are given for dissimilar operating conditions of slideways on the basis of experience. For ascertaining p_m and p_a, the first and foremost task is to determine the forces acting on the mating surfaces. Forces acting upon the mating surfaces in combination of V and flat slideways.

The combination of V and flat slideways is generally utilized in lathe machines. The schematic figure of slideways and the forces acting upon the system for the case of orthogonal cutting are demonstrated in diagram.

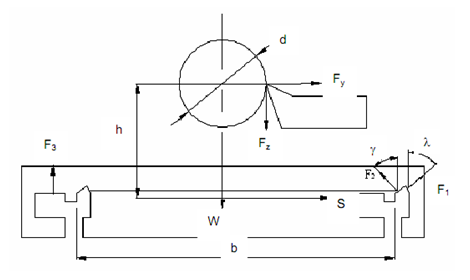
Figure: Forces Acting on Combination of V and Flat Sideways

The forces acting on V and flat slideways are :

(1) Cutting force component F_z that is in the direction of the velocity vector and F_y that is radial,

(2) Weight of carriage W, and

(3) Not known forces F₁, F₂ and F₃ acting on the mating surfaces. The unknown forces are computed from following equilibrium conditions:

Sum of components of forces acting along Y-axis = 0

i.e.

Equation 3

∑ Y = 0

F₁ sin λ - F₂ sin ϒ + F_y = 0

Sum of components of forces acting along Z-axis = 0

i.e.

Equation 4

∑ Z = 0

F₁ cos λ + F₂ cos ϒ+ F₃ - W - F_z = 0

Moment of all forces about X-axis = 0

i.e.

Equation 5

∑ M_x = 0

(F₁ cos λ. b/2) + (F₂ cos ϒ. b/2) - (F_z . d/2 ) - ( F_y . h) - (F₃. b/2) = 0

F₃ = (F₁ cos λ) + (F₂ cos ϒ) - (F_z (d/b)) - (F_y (2h/b))

Substituting value of F₃ in Eq. (4), we get,

Equation 6

(F₁ cos λ) + (F₂ cos ϒ) - (F₁ cos λ) - (F₂ cos ϒ) - (F_Z (d/b)) - (F_Y (2h / b)) - F_Z -W = 0

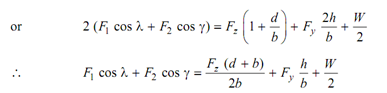
If the apex angle of the V is 90°, and suppose that present angle γ may change to γ = 90 - λ, the solution of simultaneous algebraic Eqs. No. (3) and (6) gives :

Equation 7:

F₁ = [(F_Z (d+b) / (2b)) cos λ] + [F_y (h/b) cos λ] - [F_y sin λ + (W/2) cos λ]

Equation 8:

F₂ = [(F_Z (d+b) / (2b)) sin λ] + [F_y (h/b) sin λ] - [F_y cos λ + (W/2) sin λ]

Substituting the values of F₁ and F₂ in Eq. (5) we get,

Equation 10:

F₃ = [(F_Z (b+d) / (2b))] + [F_y (h/b) + (W/2)]

Eq. (10) illustrates the forces acting upon the mating surfaces in combination of two flat sideways.

The schematic figure of the slideways and the forces acting on the system under orthogonal cutting conditions are displayed below.

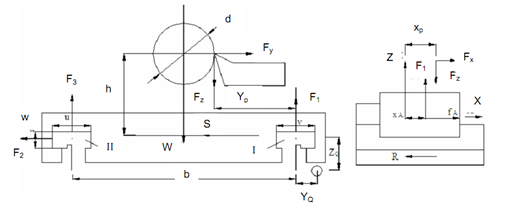
Figure: Forces Acting on Combination of Two Flat Slideways

The forces that are acting upon combination of two flat slide-ways are:

(1) Cutting force components, that are axial F_x, radial F_y, and F_z in the direction of velocity vector.

(2) Weight of carriage, W.

(3) Unknown forces F₁, F₂ and F₃ acting on the mating surfaces.

(4) Frictional forces μF₁, μF₂, μF₃, in which μ is the coefficient of friction between the sliding surfaces.

The unknown forces F₁, F₂ and F₃ are calculated from subsequent equilibrium conditions :

Equation 10

∑ X = 0

 F_x + μ (F₁ + F₂ + F₃) - R = 0

Equation 11

∑ y = 0

 F₂  - F_y  = 0

F₂ = F_y

Equation 12

∑ z = 0

 F₁  + F₃  - F_z  - W = 0

Equation 13:

∑ M_x  = 0

W (b/2) + F_Z y_P - F_y h - F₃b = 0

From Eq (13)

F₃ = ((F_zy_p - F_yh) / b)) + W/2

On substituting the value of F₃ in Eq. (12)

Equation 14

F₁ = F_z + W/2 - ((F_zy_p-F_yh) / b))

The pulling force, R is calculated from Eq. (10) on substituting the values of F₁, F₂ and F₃.

Equation 15

R = F_x  +μ (F_z  + F_y  + W )