Representation of Alternating Quantity on Complex Plane:

In complex plane, x-axis represents the real axis (reference axis) and y-axis represents the imaginary axis ( j-axis). Figure illustrates the representation of complex quantity on complex plane.

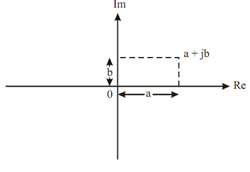
Fig: complex plane

Polar Representation

Any alternating quantity may be represented in polar form (magnitude - angle form) as under

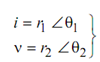
Rectangular to Polar Conversion

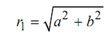
and

θ₁  = tan^-1   (b/a)

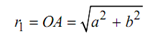
Also

and

θ₂  = tan^-1   (d/c)

In this way, rectangular quantities a + jb and c + jd can be converted into corresponding polar form, i.e.

r₁ ∠ θ₁              and           r₂  ∠ θ₂

In Figure

and θ₁ is the angle made of line OA from the horizontal axis are illustrate,

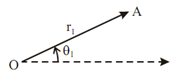
Fig

Polar to Rectangular Conversion

r₁ ∠ θ₁ may be written as :

                           r₁ e ^{j θ1} ,

Then by Euler's theorem :

r₁ e ^{j θ}₁ = r₁ [cos θ₁ + j sin θ₁ ]

         = r₁ cos θ₁ + j r₁ sin θ₁

So,

             a = r₁ cos θ₁

and      b = r₁ sin θ₁