Integrals and Summations in Physical Systems:

Differentials and derivatives arose in physical systems while little changes in one quantity were considered.  For instance, the relationship among position and time for a moving object led to the definition of the instantaneous velocity, since the derivative of the distance traveled with respect to time, ds/dt. In several physical systems, rates of change are measured straight.  Solving problems, while this is the case, includes another aspect of the mathematics of dynamic systems; namely integral & summations.

Figure is a graph of the instantaneous velocity of an object as a function of elapsed time.  This is the category of graph that could be generated if the reading of the speedometer of a car were recorded as a function of time.

At any given instant of time, the velocity of the object can be determined through referring to Figure. Therefore, if the distance traveled in a certain interval of time is to be determined, a few new methods must be used. As consider the velocity versus time curve of Figure. Let's consider the velocity changes among times t_A and t_B .The   first approach is to divide the time interval within three short intervals ( Δt₁, Δt₂, Δt₃) , and to suppose that the velocity is constant during each  of  these  intervals.  During   time interval Δt₁, the velocity is supposed constant at an average velocity v₁; during the interval Δt₂, the velocity  is assumed constant at an average velocity v₂; during time interval Δt₃, the velocity is assumed constant at an average velocity v₃.   Then

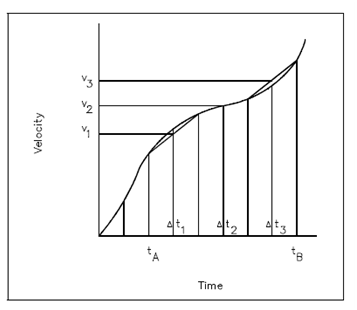
Figure: Graph of Velocity vs. Time

 the  total  distance  traveled  is approximately  the  sum  of  the products  of the  velocity  and  the elapsed time over each of the three intervals.  Equation 10 approximates the distance traveled during the time interval from t_a to t_b and represents the approximate area under the velocity curve during this same time interval.

s = v ₁  Δt₁  + v ₂    Δt₂  + v ₃   Δt₃