Resistive, Inductive and Capacitive Circuits:

AC through Pure Resistive Circuit

Applied voltage,    v = V_m  sin ωt

The resultant current, i

i = V/ R            =     (V _m  / R )sin ωt = I_m sin ωt

Current, i is in phase with applied voltage, v. The waveforms and phasor diagram are illustrated in Figures (a)and (b), respectively.

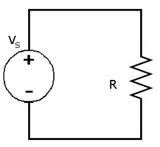
Figure: Resistive Circuit

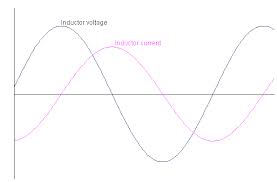
Figure: Current and Voltage Waveforms

AC through Pure Inductive Circuit

The circuit is illustrated in Figure. Again the applied voltage is given by

v = V_m  sin ωt

v = L  (di /dt)

Now,

v = V_m  sin ωt

∴          V_m sin ωt = L ( dt/ di)

∴          di = (V_m / L ) sin ωt dt

Integrating both sides, we get

 i = V_m / L ∫sin ωt dt

= V_m/ ωL (- cos ωt) = - (V_m/ ωL) cos ωt

=  (V_m /ωL) sin (ωt - (π/2))

=  (V_m/ X _L) sin ( ωt -( π /2))

where X_L = inductive reactance = ωL in ohm, if we put    V_m  / X _L = I_m , then

i = I _msin ( ωt - (π /2))