What is Factoring of Polynomials?

Factoring means much the same thing for polynomials as it does for integers. When you multiply several polynomials together,

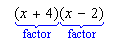
The polynomials being multiplied are called factors. If you were to multiply out these polynomials, you would get

x² + 2x - 8
This is not a factored form, because it's a sum of 3 terms. It's not in the form of several things being multiplied together.

Keep in mind that the two expressions are equivalent:
(x + 4)(x - 2) = x² + 2x - 8,

so (x + 4)(x - 2) and x² + 2x - 8, are just two different ways of writing the same thing.

Factored form: (x + 4)(x - 2)

Expanded form: x² + 2x - 8

You can say that (x + 4)(x - 2) is a factorization of

x² + 2x - 8.
There are some polynomials which are irreducible -they can't be factored. Here's an example:

x² - 5.
If you're a more advanced student, you might realize that in fact you can factor this polynomial into:

(x - √5) (x +√5)
But it is irreducible over the integers, meaning that you can't factor it into polynomials that only involve integers.

An irreducible polynomial is roughly the same thing as a prime number: it can't be factored.

A complete factorization is a factorization in which none of the factors can be broken up (factored) any further. In other words, all of the factors have to be irreducible.

Polynomials are not completely factored if there is a common factor in each term: