Question 1

Water resources in many parts of Australia are being closely watched and restrictions have been imposed on activities such as garden watering. Suppose that SA Water monitors water usage in an Adelaide suburb and finds that for one summer the average household usage is 408 litres per day. A year later it examines records for a randomly selected sample of 50 households and finds that there is a daily mean usage of 380 litres with a standard deviation of 25 litres.

(a) Construct and interpret a 95% confidence interval for the population mean daily water usage in the second summer. Does the population have to be Normal here? Explain.

(b) Do you think water usage has changed in the second summer? Explain.

Question 2

David, Diana and Lydia are the sole partners and workers in a company that produces fine clocks. David and Diana are each available to work a maximum of 40 hours per week at the company, while Lydia is available to work a maximum of 20 hours per week.

The company makes two different types of clocks: a grandfather clock and a wall clock. To make a clock, David (a mechanical engineer) assembles the inside mechanical parts of the clock while Diana (a woodworker) produces the hand carved wood casings. Lydia is responsible for taking orders and shipping the clocks. The amount of time required for each of these tasks is shown below.

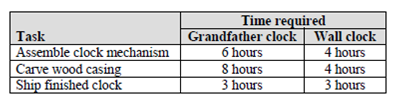
Each grandfather clock built and shipped yields a profit of $300, while each wall clock yields a profit of $200.

The three partners now want to determine how many clocks of each type should be produced per week to maximize the total profit using linear programming. They have asked for your help.

(a) Formulate a linear programming model for this problem. In doing so, consider the following:

1. What are the decision variables for this problem?

2. What is the objective for this problem? Using your decision variables, formulate the objective function.

3. What are the constraints in this problem? Using your decision variables, formulate these constraints.

(b) Use EXCEL Solver to obtain a solution to the linear programming problem from part (a), together with an Answer Report and a Sensitivity Report. Provide a copy of your EXCEL spreadsheet and of the two Excel reports in your assignment submission.

EXCEL Instructions: All EXCEL output should bear your ID number.

Your inserted output should be titled 'FamilyName,GivenName,ID'

Please refer to Topic 5 in the Excel Booklet or the Linear Programming Supplement to the textbook (pdf file posted on the course resources website) for detailed instructions on how to set up your spreadsheet and use Solver. You may use the Excel file on the portal as a template.

(c) Grandfather clocks have become very popular and the partners feel that a unit profit per grandfather clock of $375 may be possible. Would the solution obtained in part

(b) still be optimal? Which of the EXCEL reports helps you answer this question? Justify your answer carefully. How would the total profit change, if at all?

(d) Prepare a report that summarizes your linear programming results. Your report should discuss the following:

1. The optimal number of grandfather and wall clocks, as well as the maximum total profit.

2. Resulting work hours for each of the partners. How do these compare to the maximum hours each partner is able to allocate to this business?

3. Profit per unit considerations from part (c).

Report Instructions: Your report should be at most one page, in 12pt Times New Roman or a similar font, with 1.5 line spacing and at least 2cm margins.