Varignon theorem:
State Varignon's theorem. How it helps in determining of the moments? In which type of condition is it used?
Sol.: Varignon's theorem also called Law of Moment.
The application of varignon's theorem practically is to find the position of the resultant from any point of the body.
It states "If number of coplanar forces is acting simultaneously on a particle, algebraic sum of moments of all the forces about any point is equal to moment of their resultant force about same point."
Proof: Let us consider, two concurrent forces P and Q represented in magnitude and direction by AB and AC as shown in the figure given below.
Let 'O' be the point, about which moment are taken, through O draw line OD parallel to direction of force P, to meet line of action of force Q at point C. Now with AB and AC as the two adjacent sides, complete Parallelogram ABDC as shown in the figure given below. Join the diagonal AD of the parallelogram and OA and OB. From parallelogram law of forces, we know that diagonal AD represents in the magnitude and direction, resultant of two forces P and Q. Now we see that moment of the force P about O: = 2. Area of triangle AOB ...(i)
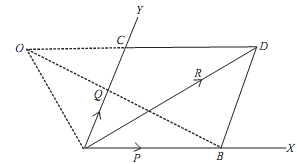
Likewise, moment of the force Q about O: = 2. Area of ΔAOC ...(ii)
And moment of resultant force R about O: = 2.Area of ΔAOD ...(iii)
But from the geometry of the figure, we find that
Area of ΔAOD = Area of ΔAOC + Area of ΔACD
But the Area of ΔACD = Area of ΔABD = Area of ΔAOB
(As the two "AOB and ADB are on same base AB and between same // lines)
Now Area of triangle AOD = Area of triangle AOC + Area of triangle AOB
Multiply both the side by 2 we obtain;
2. Area of triangle AOD = 2.Area of triangle AOC + 2. Area of triangle ACD, that gives
Moment of force R about O = Moment of force P about O + Moment of force Q about O or,
Where R . d = ∑M
∑M = Sum of moment of all the forces
d = Distance between resultant force and point where moment of all the forces are taken. This principle can be extended for any number of the forces.