Suppose that we know the logarithms of all numbers which are expressed to base 'a' and we are required to find the logarithms of all these numbers to base 'b'. We proceed as follows. Let N be any one of the numbers of which we are required to find the logarithm to base 'b' and the value itself be some 'x'. That is, log_bN = x or N = b^x. But we already know the value of log_a N. Also log_aN can be expressed as log_a(b^x) as N = b^x. By rule 5, log_a(b^x) can be expressed as x.log_ab or 

         xlog_ab = log_aN

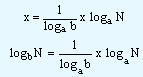                   ...............(1)

Since the values of N and b are known, the values of log_a N and log_a b can be found from the tables. These values when substituted in equation (1) gives us the value of log_b N.

In the above equation, what will happen if N = a. Equation (1) will be

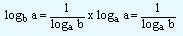(because logaa = 1)

or

         log_ba x log_a b = 1

Example 

Find the values of the following.

1. log₃ 81

We know that 81 = 3⁴. Therefore, log₃ 3⁴ = 4. log₃ = 4.1 = 4

1. log₃ (9 x 27 x 81)

         log₃ (9 x 27 x 81) = log₃9 + log₃27 +  log₃81

                                           (log_a M.N = log_a M + log_aN)

                                        = log₃(3²) + log₃(3³) + log₃(3⁴)

                                        = 2.log₃3 + 3.log₃3 + 4.log₃3

                                        = 2 + 3 + 4 = 9

1. log3 4√35

In this example we apply an extension of rule 5.

(5/4).log₃3 = (5/4).1 = (5/4)

1. log₃ (243/81)

         log₃243 - log₃81 [log_a (M/N) = log_aM - log_a N]

         log₃3⁵ - log₃3⁴

         5.log₃3 - 4.log₃3 = 5 - 4 = 1

         (log_M (M^P) = p.log_M M = p)