Tests for heteroscedasticity, Advanced Statistics

Assignment Help:

Lagrange Multiplier (LM) test

The Null Hypothesis - H0: There is no heteroscedasticity i.e. β₁ = 0

The Alternative Hypothesis - H1: There is heteroscedasticity i.e. β₁ 0

Reject H0 if nR2 > 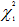2094_Tests for Heteroscedasticity.png

Regression Analysis: sqresi versus sqfits

The regression equation is

sqresi = 0.00517 + 0.0196 sqfits

Predictor Coef SE Coef T P VIF

Constant 0.005173 0.001130 4.58 0.000

sqfits 0.019650 0.008395 2.34 0.019 1.000

S = 0.0112996 R-Sq = 0.4% R-Sq(adj) = 0.3%

Analysis of Variance

Source DF SS MS F P

Regression 1 0.0006996 0.0006996 5.48 0.019

Residual Error 1500 0.1915214 0.0001277

Lack of Fit 646 0.0819554 0.0001269 0.99 0.559

Pure Error 854 0.1095659 0.0001283

Total 1501 0.1922209

MTB > let k1 = 1502*0.04

MTB > print k1

Data Display

K1 60.0800

Inverse Cumulative Distribution Function

Chi-Square with 1 DF

P( X <= x ) x

0.95 3.84146

Since nR2 = (1502*0.04) 60.0800 > 3.84146 = 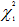2094_Tests for Heteroscedasticity.png , there is sufficient evidence to reject H0 which suggest that there is heteroscedasticity from the Lagrange Multiplier (LM) test at 5% significance level which means that one or more slopes are not zero.

Related Discussions:- Tests for heteroscedasticity

Operations Management, 1.Sam Lucarelli, owner of Lucarelli Products, is eva...

1.Sam Lucarelli, owner of Lucarelli Products, is evaluating whether to produce a new product line. After thinking through the production process and the costs of raw materials and

Catastrophe theory, Catastrophe theory : A theory of how little is the cont...

Catastrophe theory : A theory of how little is the continuous changes in the independent variables which can have unexpected, discontinuous effects on the dependent variables. Exam

OPERATIONS RESEARCH, CONSTRUCTION OF AN OR MODEL

CONSTRUCTION OF AN OR MODEL

Common cause failures (ccf), Common cause failures (CCF): Simultaneous fai...

Common cause failures (CCF): Simultaneous failures of the number of components due to a same reason. A reason can be external to the components, or it can be the single failure wh

Dropout, A subject who withdraws from the study for whatever reason, advers...

A subject who withdraws from the study for whatever reason, adverse side effects, noncompliance, moving away from the district, etc. In number of cases the reason may not be known.

Empirical likelihood, An approach of using the likelihood as the basis of e...

An approach of using the likelihood as the basis of estimation without the requirement to specify a parametric family for data. Empirical likelihood can be viewed as the example of

Queuing theory, 1) Let N1(t) and N2(t) be independent Poisson processes wit...

1) Let N1(t) and N2(t) be independent Poisson processes with rates, ?1 and ?2, respectively. Let N (t) = N1(t) + N2(t). a) What is the distribution of the time till the next epoch

Adjusted r-squared, R-squared is regarded as the coefficient of determinati...

R-squared is regarded as the coefficient of determination and is used to give the proportion of the fluctuation of the variance of one variable to another variable. R-squared also

Quantitative, How has quantitative analysis changed the current scenario in...

How has quantitative analysis changed the current scenario in the management world today?

Collective risk models, Collective risk models : The models applied to insu...

Collective risk models : The models applied to insurance portfolios which do not create direct reference to the risk characteristics of individual members of the portfolio when des

Write Your Message!

Name

Email id

Message

Verfication Code

User Account

All Pages