Tests for Consistency
The consistency of the index numbers have been tested over the years. The most important of these tests are:
-
The time reversal test
-
The factor reversal test
-
The circular test.
Time Reversal Test
Time reversal test has been developed by Prof. Irving Fisher. The test implies that for a price/quantity index, if the time periods are reversed, the resulting index should be the reciprocal of the original price/quantity index.
If I0,1 denotes the original index for the current year with a given base year, and if I1, 0 denotes the resulting index, with time periods reversed, for the base year with the current year as a base year, then according to the time reversal test,
|
I0, 1 =
|
 |
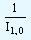(or) I0, 1 x I1, 0 = 1 |
Let us test the consistency of the indices by interchanging 0 and 1 with 1 and 0 respectively.
It can be shown that Fisher's Ideal Index, Marshall-Edgeworth Index and Fixed Weights Aggregate Index satisfy this test. Laspeyres Index and Paasche Index do not.
Factor Reversal Test
This test was also suggested by Prof. Irving Fisher. According to Prof. Fisher just as each formula should permit the interchange of the two time periods without giving inconsistent results, it ought to permit interchanging of the prices and quantities without giving inconsistent result, i.e. the two results multiplied together should give the true value ratio.
The product of change in prices in the current year and the change in quantities in the current year should be equal to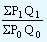 
(Value ratio)
where,
P1=Prices in the current year
P0=Prices in the base year
Q1=Quantities in the current year
Q0=Quantities in the base year
The test can be applied to the index numbers by interchanging P to Q and Q to P.
Except Fischer's Ideal Index, all other elementary indices, simple as well as weighted, fail to satisfy this test.
Circular Test
Circular test is an extension of the time reversal test. This test is used while measuring price changes over a number of years with the shifting of base occurring frequently. According to this test, an index constructed for the year 'X' on base year 'Y' and for the year 'Y' on base year 'Z' should yield the same result as an index constructed for 'X' on base year 'Z'.
i.e. I0,1 x I1,2 x I2,0 = 1.
Laspeyres, Paasche and Fisher's indices fail to satisfy this test. Only the fixed weight aggregates method and simple aggregates method satisfy this test.
The indices satisfying the circular test would be amenable to change from year to year without referring to the base year. The indices have the advantage of reduced computational work in the event of a change in the base year.