Test of hypothesis about the difference among two means

The t test can be utilized under two assumptions when testing hypothesis about the difference among the two means; that the two are normally distributed as or near normally distributed populations and that the standard deviation of the two is the similar or at any rate not significantly different.

Appropriate test statistic to be utilized is

      t     = (x¯₁ - x¯₂)/S_{(x¯1 - x¯2)}           at (n1 + n2 - 2) d.f.

The standard deviation is acquired by pooling the two sample standard deviation as given below likes:

Sp =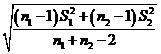

Whereas S₁ and S₂ are standard deviation for sample 1 & 2 respectively

Now S_x¯1 = Sp/√n₁   and S_x¯2=  Sp/√n₂  

 S_{(x¯1 - x¯2)}=  √{ S²_x¯1 + S²_x¯2 }

Alternatively S_{(x¯1 - x¯2)}=  Sp √{(n₁ + n₂)/n₁n₂}

Illustration

Two different types of drugs A and B were tried on specific patients for increasing weights, 5 persons were provided drug A and 7 persons were provided drug B. the increase in weight in pounds is described below as:

Do the two drugs differ significantly along with regard to their effect in increasing weight? As described that v= 10; t0.05 = 2.23

Solution

H₀ : μ₁ = μ₂

H₁ : μ₁ ≠ μ₂

t =  (x¯₁ - x¯₂)/S_{(x¯1 - x¯2)}

Calculate for x¯₁ , x¯₂  and S

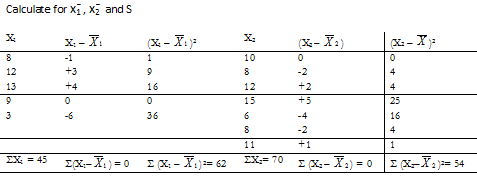
X₁ = åx₁/n₁  = 45/5 = 9 ; X₂ = åx₂/n₂ = 70/7 = 10 ;

S₁ = √(62/4) = 3.94 ;  S₂ = √(54/6) = 3;

S_p = {((4 * 15.4) + (6 * 9))/10}

= 3.406

S_{(x¯1 - x¯2)} = √{(11.6/5) + (11.6/7)}

= 1.99

t = (x¯₁ - x¯₂)/S_{(x¯1 - x¯2)}

 = ¦{(9 - 10)/1.99}¦

= 0.50

Now t0.05 (at v = 10) = 2.23 > 0.5

Thus we accept the null hypothesis.

Hence there is no significant difference in the efficacy of the two drugs in the matter of increasing weight