Recall also which value of the derivative at a specific value of t provides the slope of the tangent line to the graph of the function at that time, t. Thus, if for some time t the velocity occurs to be 30 m/s the slope of the tangent line to the graph of the velocity is 3.92.

We could carry on in this fashion and pick various values of v and calculate the slope of the tangent line for such values of the velocity. Although, let's take a slightly additionally organized approach to that. Let's first identify the values of the velocity which will have zero slope or horizontal tangent lines. These are easy adequate to determine. All we require to do is set the derivative equivalent to zero and resolve for v.

In the case of our illustration we will have only one value of the velocity that will have horizontal tangent lines, v = 50 m/s. What it means is that IF (again, there's that word if), for several time t, the velocity occurs to be 50 m/s after that the tangent line at that point will be horizontal. What the slope of the tangent line is at times before and after this point is not identified yet and has no bearing on the slope at this exact time, t.

Thus, if we have v = 50, we identify that the tangent lines will be horizontal. We indicate this on an axis system along with horizontal arrows pointing toward increasing t at the level of v = 50 as demonstrated in the subsequent figure.

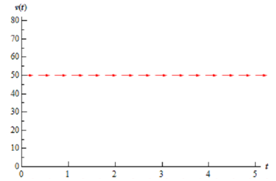
Here, let's find some tangent lines and thus arrows for our graph for some another value of v. At that point the only precise slope that is helpful to us is where the slope horizontal. Consequently instead of going after exact slopes for the rest of the graph we are only aimed at go after general trends in the slope. Is the slope decreasing or increasing? How quick is the slope decreasing or increasing? For this illustration those kinds of trends are extremely easy to find.