Not every linear system along with three equations and three variables utilizes the elimination method exclusively therefore let's take a look at another instance where the substitution method is used, at least partially.
Example Solve the given system of equations.
2 x - 4 y + 5z = -33
4 x - y = -5
-2 x +2 y - 3z = 19
Solution
Before we get started on the solution procedure do not get excited regarding the fact that the second equation just has two variables in it. That is a fairly common occurrence while we have more than two equations into the system.
Actually, we're going to take advantage of the fact that it only has two variables and one of them, the y, has a coefficient of -1. This equation is simply solved for y to get,
y = 4 x + 5
Then we can substitute this into the first & third equation as follows,
2x - 4 ( 4x + 5) + 5z = -33
-2x + 2 ( 4 x + 5) - 3z= 19
Now, if you think regarding it, it is just a system of two linear equations along with two variables (x & z) and we know how to solve out these kinds of systems from our work in the previous section.
Firstly, we'll have to do a little simplification of the system.
2x -16x - 20 + 5z = -33 -14x + 5z = -13
→
-2x+ 8x + 10 - 3z = 19 6x - 3z = 9
The simplified version looks like the systems we were solving out in the previous section. Well, it's almost the similar. The variables this time are x & z rather than x and y, however that really isn't a difference. The work of solving this will be the simlar.
We can utilize either the method of substitution or the method of elimination to solve out this new system of two linear equations.
If we desired to use the method of substitution we could simply solve the second equation for z (you do illustrates why it would be easiest to solve out the second equation for z right?) and substitute that in the first equation. This would let to determine x and then we could determine both z and y.
Though, to make the point that frequently we use both methods in solving out systems of three linear equations let's employ the method of elimination to solve out the system of two equations. We'll just have to multiply the first equation by 3 and the second by five. Doing this gives,
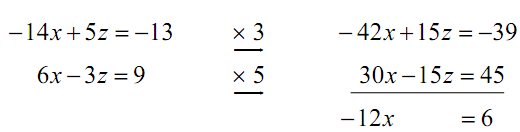
Now we can easily solve for x to get x = - 1/2. The coefficients on the second equation are smaller hence let's plug this into that equation and solve out for z. Following is that work.
6 ( -1/2) - 3z = 9
-3 - 3z = 9
-3z = 12
z = -4
At last, we have to determine the value of y. It is very easy to do. Remember again in the first step we utilized substitution and in that step we utilized the following equation.
y = 4 x + 5
As we know the value of x all we have to do is plug that into this equation & get the value of y.
y = 4 ( - 1/2 ) + 5 = 3
Note that in several cases where we utilized substitution on the very first step the equation you'll contain at this step will contain both x's & z's and hence you will require both values to get the third variable.
To end this example up here is the solution: x = - 1 /2 , y = 3 and z = -4 .
As we've seen with the two examples above there are a variety of paths that we could select to take while solving a system of three linear equations along with three variables. This will always be the case. There is no one true path for solving out these. Though, having said that there is frequently a path that will let you to avoid some of the mess that can arise in solving these types of systems. Once you work sufficient of these kinds of problems you'll begin to get a feel for a "good" path through the solution procedure that will (hopefully) ignore some of the mess.
In these cases Interpretation of solutions is a little harder into some senses. In the examples all three of these equations above are equations of planes in three dimensional space & solution to this systems in the instance above is the one point that all three of the planes have in common.
Note as well that it is totally possible to have no solutions to these systems or infinitely many systems as we illustrated in the previous section along with systems of two equations.